If Δ1=∣∣ ∣∣xbbaxbaax∣∣ ∣∣ a n d Δ2=∣∣∣xbax∣∣∣ are the given determinants, then Δ1=3(Δ2)2 b.ddx(Δ1)=3Δ2 c. ddx(Δ1)=3(Δ2)2 d. Δ1=3(Δ2)3/2Solution in Bengali
Δ1=3(Δ2)2
ddx(Δ1)=3Δ2
ddx(Δ1)=3(Δ2)2
Δ1=3Δ3/22
The correct Answer is:B
(b) Δ1=x(x2−ab)−b(ax−ab)+b(a2−ax)
=x3−3abx+ab2+a2b
∴ddx(Δ1)=3x2−3ab=3(x2−ab)=3Δ2
Topper's Solved these Questions
- DETERMINANTBOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DETERMINANTBOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTEXERCISE - Multiple Correct Answer
5 Videos
- DEFINITE INTEGRATION BOOK - CENGAGE PUBLICATIONCHAPTER - DEFINITE INTEGRATION EXERCISE - JEE ADVANCED
38 Videos
- DETERMINANTSBOOK - CENGAGE PUBLICATIONCHAPTER - DETERMINANTSEXERCISE - All Questions
262 Videos
Similar Questions
If x∈R,ai,bi,ci∈R for i=1,2,3 and ∣∣ ∣∣a1+b1xa1x+b1c1a2+b2xa2x+b2c2a3+b3xa3x+b3c3∣∣ ∣∣=0, then which of the following may be true ?
View SolutionIf x∈R,ai,bi,ci∈R for i=1,2,3 and ∣∣ ∣∣a1+b1xa1x+b1c1a2+b2xa2x+b2c2a3+b3xa3x+b3c3∣∣ ∣∣=0, then which of the following may be true ?
View SolutionLet f be a non-negative function defined on the interval [0,1]. If ∫x0√1−(f′(t))2dt=∫x0f(t)dt,0≤x≤1,and f(0)=0, then
View SolutionIf P = {1,2}, form set set P×P×P
View SolutionIf Δ1=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣ and Δ2=∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣, without expending or evaluating Δ1andΔ2 , show that Δ1+Δ2=0
View SolutionIf Δ1=∣∣ ∣ ∣∣111abca2b2c2∣∣ ∣ ∣∣,Δ2=∣∣ ∣∣1bca1cab1abc∣∣ ∣∣,then Δ1+Δ2=0 (b) Δ1+2Δ2=0 Δ1=Δ2 (d) none of these
View SolutionDelta_1 = |[x,b,b], [a,x, b] ,[a, a, x]| and Delta_2 = |[x,b],[a,x]| show that d(Delta_1)/ dx = 3 Delta_2
View SolutionIf x^a y^b=e^m , x^c y^d=e^n ,Delta_1=|(m,b),(n,d)|,and Delta_2 =|(a,m),(c,n)| and Delta_3=|(a,b),(c,d)|, then the values of x and y are
View SolutionIf Δ1=∣∣ ∣∣104317744−57∣∣ ∣∣,Δ2=∣∣ ∣∣4x+537x+124−5x−17∣∣ ∣∣ such that Δ1+Δ2=0, then
View SolutionIf Δ1=∣∣∣10ab∣∣∣ and Δ2=∣∣∣10cd∣∣∣, then Δ2Δ1 is equal to :
View SolutionIf
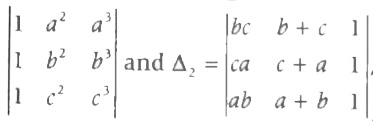 then Δ1Δ2=
then Δ1Δ2=
View SolutionΔ1=∣∣ ∣∣xbaaxbaax∣∣ ∣∣,Δ2=∣∣∣xbax∣∣∣ are the given determinants , then :
View SolutionIf Δ1=∣∣ ∣ ∣∣abcxyzpqr∣∣ ∣ ∣∣ and Δ2=∣∣ ∣ ∣∣q−by−pa−xr−cz∣∣ ∣ ∣∣, without expanding or evaluating Δ1andΔ2 , show that Δ1+Δ2=0
View SolutionIf Δ1=∣∣ ∣ ∣∣111abca2b2c2∣∣ ∣ ∣∣,Δ2=∣∣ ∣∣1bca1cab1abc∣∣ ∣∣,then (a)Δ1+Δ2=0 (b) Δ1+2Δ2=0 (c)Δ1=Δ2 (d) none of these
View SolutionIf Δ1=∣∣ ∣∣xbbaxbaax∣∣ ∣∣andΔ2=∣∣∣xbax∣∣∣ are given determinants then,
View SolutionIf Δ1=∣∣ ∣∣xabbxaabx∣∣ ∣∣andΔ2=∣∣∣xaax∣∣∣ are the given determinants , then
View Solution
