If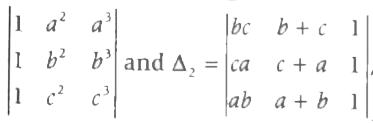 
then Δ1Δ2=
ab + bc + ca
abc
2(ab + bc+ ca)
(a+b+c)2
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
If Δ1=∣∣ ∣∣b+cc+aa+bc+aa+bb+ca+bb+cc+a∣∣ ∣∣ and Δ2=∣∣ ∣∣abcbcacab∣∣ ∣∣ then Δ1Δ2=_______
View Solutionα, β, γ are the roots of the equation x3−7x2+bx+5=0. If Δ1 is the area of the triangle formed by (α,α3), (β,β3), (γ,γ3), Δ2 is the area of the triangle formed by (α,α2), (β,β2), (γ,γ2) then Δ1Δ2=
View Solution
Knowledge Check
If Δ1 is the area of the triangle formed by the centroid and two vertices of a triangle Δ2 is the area of the triangle formed by the mid- point of the sides of the same triangle, then Δ1:Δ2=
A3:4B4:1C4:3D2:1
Δ1=∣∣ ∣ ∣∣e2bh6d12a6g3f6c3i∣∣ ∣ ∣∣,Δ2=∣∣ ∣ ∣∣2a2c2b3g3i3h−d−f−e∣∣ ∣ ∣∣. If Δ2≠0 then Δ1Δ2 is equal to
View SolutionIf the two quadratic ax2+bx+c=0 and lx2+mx+n=0 have roots α,β and γ,δrespectively. If α,β,γ and δ are in A.P and Δ1 and Δ2 be the discriminants of these quadratics then Δ1Δ2 is
View SolutionIf Δ1 and Δ2 are respectively areas of incircle and circumcircle of triangle formed by (0,0),(2,0) and (1,√3), then Δ2Δ1=?
View Solutionα,β,γ are the roots of the equation x3−7x2+bx+5=0. If Δ1 is the area of the triangle formed by (α,α3),(β,β3),(γ,γ3),Δ2 is the area of the triangle formed by (α,α2),(β,β2),(γ,γ2)then Δ1Δ2=
View SolutionConsider the parabola y2=8x. Let Δ1 be the area of the triangle formed by the end points of its latus rectum and the point P(12,2) on the parabola, and Δ2 be the area of the triangle formed by drawing tangents at P and at the end points of the latus rectum. Then Δ1Δ2 is
View SolutionLet A(0,-1),B(0,3)andC(2,1) be three points Let Δ1 be the area of the triangle ABC and Δ2 be the area of the triangle formed by the mid points of the sides of the triangle whose vertices are A,B and C such that Δ1Δ2=1x Find the value of x.
View SolutionConsider the parabola y2=8x. Let △1 be the area of the triangle formed by the endpoints of its latus rectum and the point P(12,2) on the parabola, and △2 be the area of the triangle formed by drawing tangents at P and at the endpoints of the latus rectum. Then is Δ1Δ2 is.
View Solution