If ΔABC is an equilateral triangle such that AD⊥BC,AD2=kDC2 , then k is
The correct Answer is:k=3
To solve the problem, we need to find the value of k given that AD2=k⋅DC2 in an equilateral triangle ΔABC where AD is perpendicular to BC.
1. Draw the Equilateral Triangle:
- Start by sketching an equilateral triangle ΔABC with all sides equal. Let AB=BC=CA=a.
2. Identify the Perpendicular:
- Draw the altitude AD from vertex A to side BC. This creates two right triangles, ΔABD and ΔACD.
3. Apply the Pythagorean Theorem:
- In triangle ΔACD, we apply the Pythagorean theorem:
AC2=AD2+DC2
- Since AC=a (as all sides are equal), we can rewrite this as:
a2=AD2+DC2
4. Express AD2:
- Rearranging the equation gives:
AD2=a2−DC2
5. Relate AD2 and DC2:
- We know from the problem statement that:
AD2=k⋅DC2
- Substituting for AD2 from the previous step gives:
k⋅DC2=a2−DC2
6. Rearranging the Equation:
- Rearranging the equation to isolate k:
k⋅DC2+DC2=a2
(k+1)DC2=a2
7. Express k:
- Dividing both sides by DC2 (assuming DC≠0):
k+1=a2DC2
- Thus,
k=a2DC2−1
8. Find the Relationship Between a and DC:
- In an equilateral triangle, the altitude AD can be expressed in terms of the side a:
AD=√32a
- Using the properties of the triangle, we find that DC=12a.
9. Substituting DC:
- Substitute DC=12a into the equation:
k=a2(12a)2−1
k=a214a2−1
k=4−1
k=3
Final Answer:
Thus, the value of k is 3.
---
- Start by sketching an equilateral triangle ΔABC with all sides equal. Let AB=BC=CA=a.
- Draw the altitude AD from vertex A to side BC. This creates two right triangles, ΔABD and ΔACD.
- In triangle ΔACD, we apply the Pythagorean theorem:
AC2=AD2+DC2
- Since AC=a (as all sides are equal), we can rewrite this as:
a2=AD2+DC2
- Rearranging the equation gives:
AD2=a2−DC2
- We know from the problem statement that:
AD2=k⋅DC2
- Substituting for AD2 from the previous step gives:
k⋅DC2=a2−DC2
- Rearranging the equation to isolate k:
k⋅DC2+DC2=a2
(k+1)DC2=a2
- Dividing both sides by DC2 (assuming DC≠0):
k+1=a2DC2
- Thus,
k=a2DC2−1
- In an equilateral triangle, the altitude AD can be expressed in terms of the side a:
AD=√32a
- Using the properties of the triangle, we find that DC=12a.
- Substitute DC=12a into the equation:
k=a2(12a)2−1
k=a214a2−1
k=4−1
k=3
Thus, the value of k is 3.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Olympiad /HOTS Corner15videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLES EXERCISE - Exercise (Subjective Problems) (Long Answer Type)7videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - OLYMPIAD/HOTS CORNER20videos
SURFACE AREAS AND VOLUMES
Similar Questions
Knowledge Check
- Question 1 - Select One
ΔABC is an equilateral triangle such that AD⊥ BC, then AD2=
A32DC2B2DC2C3CD2D4DC2 - Question 2 - Select One
If ABC is an equilateral triangle and D is a point on BC such that AD⊥BC, then
AAB:BD=1:1BAB:BD=1:2CAB:BD=2:1DAB:BD=3:2 - Question 3 - Select One
In the figure ΔABE is an equilateral triangle in a square ABCD. Find the value of angle x in degrees :
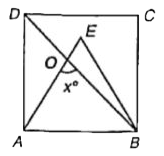 A60∘B45∘C75∘D90∘
A60∘B45∘C75∘D90∘
Prove that in a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
Use the above theorem, in the following.
If ABC is an equilateral triangle with AD⊥BC, then prove that AD2=3DC2.View SolutionΔABC is an equilateral triangle. Point D is on side BC such that BD=15BC then prove 25AD2=21AB2.
View SolutionIn equilateral △ABC,AD⊥BC. Prove that 3BC2=4AD2.
View Solution
Triangle ABC is an equilateral triangle. If ∠ADE=30∘, then find ∠AED.View SolutionWhat is the ratio of the areas of ΔABC and ΔBDE , if ΔABC and ΔBDE are two equilateral triangles such that D is the mid-point of BC.
View Solution

