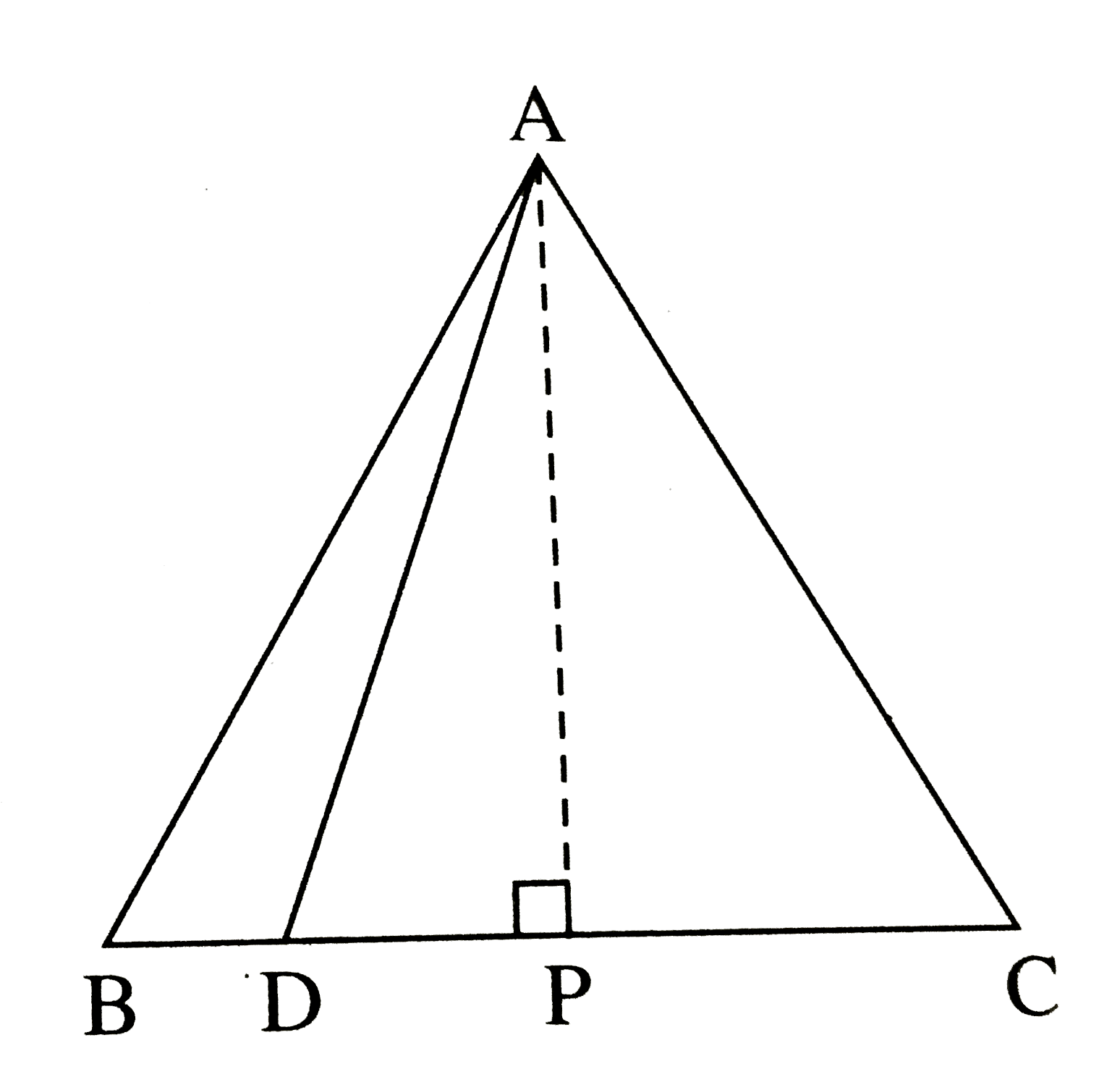
$Δ A B C$ is an equilateral triangle. Point $D$ is on side $B C$ such that $B D = \frac{1}{5} B C$ then prove $25 A D^{2} = 21 A B^{2}$ .

Video Solution

Text Solution

Verified by Experts

Draw seg $A P ⊥$ side $B C$ such that $B - P - C$ .
In $Δ A P B$ ,
$∠ A P B = 90^{\circ}$ …..(Construction)
$∠ A B P = 60^{\circ}$ …..(Angle of an equilateral triangle)
$∴ ∠ B A P = 30$ ……..(Remaining angle of a triangle)
$∴ Δ A P B$ is a $30^{\circ} - 60^{\circ} - 90^{\circ}$ triangle
$A P = \frac{\sqrt{3}}{2} A B$ .......(Side opposite to $60^{\circ}$ )...... $(1)$
$B P = B D + D P$ ....... $(B - D - P)$
$∴ B P = \frac{1}{5} B C + D P$ ......( $B D = \frac{1}{5} B C$ , given)
$∴ \frac{1}{2} B C = \frac{1}{2} B C + D P$ .......(In an equilateral triangle, the perpendicular from a vertex bisects the opposite side)
$∴ D P = \frac{1}{2} B C - \frac{1}{5} B C$
$∴ D P = \frac{5 B C - 2 B C}{10} = \frac{3 B C}{10} = \frac{3 A B}{10}$ ......... $(2)$
( $∵ B C = A B$ , side of equilateral triangle)
In $Δ A P D$ ,
$∠ A P D = 90^{\circ}$ ......(Construction)
$∴$ By Pythagoras theorem
$A D^{2} = A P^{2} + D P^{2}$
$∴ A D^{2} = {(\frac{\sqrt{3}}{2} A B)}^{2} + {(\frac{3 A B}{10})}^{2}$ ......]From $(1)$ and $(2)$ ]
$∴ A D^{2} = \frac{3}{4} A B^{2} + \frac{9 A B^{2}}{100}$
$∴ A D^{2} = \frac{75 A B^{2} + 9 A B^{2}}{100}$
$∴ A D^{2} = \frac{84 A B^{2}}{100}$
$∴ A D^{2} = \frac{21 A B^{2}}{25}$
$∴ 25 A D^{2} = 21 A B^{2}$

Updated on:21/07/2023