IF E1E2E3……..E10 are the possible elementary events of a random experiment , then
P(E1)+P(E2)+P(E3)+……P(E10) is equal to
0
1
2
3
The correct Answer is:B
Topper's Solved these Questions
- CPC MODEL QUESTION PAPER -6Book:CPC CAMBRIDGE PUBLICATIONChapter:CPC MODEL QUESTION PAPER -6Exercise:QUESTION
Explore 30 Videos
- CO-ORDINATE GEOMETRYBook:CPC CAMBRIDGE PUBLICATIONChapter:CO-ORDINATE GEOMETRYExercise:EXERCISE 7.4
Explore 6 Videos
- CPC MODEL QUESTION PAPER 5Book:CPC CAMBRIDGE PUBLICATIONChapter:CPC MODEL QUESTION PAPER 5Exercise:VI. Answer the following :
Explore 1 Video
Similar Questions
Suppose E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2E1)=12 and P(E1E2)=14 then P(E2)=
View SolutionIf E1andE2 are two events associated with a random experiment such that P(E2)=0.35,P(E1orE22)=0.85andP(E1andE2)=0.15, then P(E1) is (A) .25 (B) .35 (C) .65 (D) .75
View Solution
Knowledge Check
If E and F are independent events, P(E)=12 and P(F)=13, then P(E∩F) is :
A12B13C0D16Let E1 and E2 are the two independent events such that P(E1)=0.35 and P(E1∪E2)=0.60, find P(E2).
A413B513C613D713Statement -1 : Let E1,E2,E3 be three events such that P(E1)+P(E2)+P(E3)=1, then E1,E2,E3 are exhaustive events.
Statement-2 if the events E1,E2 and E3 be exhaustive events, then P(E1∪E2∪E3)=1AStatement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for statement -9BStatement-1 is true, Statement-2 is true, Statement-2 is Not a correct explanation for statement -9CStatement-1 is true, Statement-2 is FalseDStatement-1 is False, Statement-2 is true
Suppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
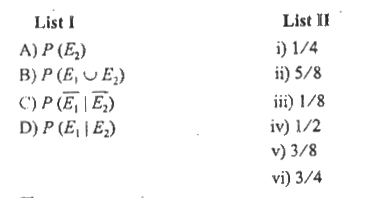
The correct matching of the list I from the list II is :
View SolutionIf E be an event such that P(E)=37 , what is P( not E ) equal to ?
View SolutionIf e1,e2,e3 and e4 are the four elementary outcomes in a sample space and P(e1)=0.1,P(e2)=0.5,and P(e3)=0.1, then the probability of e4 is ……
View SolutionIf e1,e2,e3 and e4 are the four elementary outcomes in a sample space and P(e1)=0.1,P(e2)=0.5,and P(e3)=0.1, then the probability of e4 is ……
View SolutionIf E1 nad E2 are two independent events such that P(E1)=0.3 and P(E2)=0.6 then find the value of (i)P(E1∩E2) (ii) P(E1∪E2) (iii)P(E1E2) (iv) P(E2E1)
View Solution
