If are the four elementary outcomes in a sample space and then the probability of is ……
To find the probability of the fourth elementary outcome e4, we can follow these steps:
1. Understand the Concept of Probability in a Sample Space:
In a sample space, the sum of the probabilities of all elementary outcomes must equal 1. This means:
P(e1)+P(e2)+P(e3)+P(e4)=1
2. Identify the Given Probabilities:
From the question, we have:
P(e1)=0.1,P(e2)=0.5,P(e3)=0.1
3. Substitute the Known Values into the Equation:
We can substitute the known probabilities into the equation:
0.1+0.5+0.1+P(e4)=1
4. Calculate the Sum of the Known Probabilities:
First, calculate the sum of P(e1), P(e2), and P(e3):
0.1+0.5+0.1=0.7
5. Solve for P(e4):
Now, substitute this sum back into the equation:
0.7+P(e4)=1
To find P(e4), subtract 0.7 from both sides:
P(e4)=1−0.7=0.3
6. Conclusion:
Therefore, the probability of e4 is:
P(e4)=0.3
Final Answer:
The probability of e4 is 0.3.
---
In a sample space, the sum of the probabilities of all elementary outcomes must equal 1. This means:
P(e1)+P(e2)+P(e3)+P(e4)=1
From the question, we have:
P(e1)=0.1,P(e2)=0.5,P(e3)=0.1
We can substitute the known probabilities into the equation:
0.1+0.5+0.1+P(e4)=1
First, calculate the sum of P(e1), P(e2), and P(e3):
0.1+0.5+0.1=0.7
Now, substitute this sum back into the equation:
0.7+P(e4)=1
To find P(e4), subtract 0.7 from both sides:
P(e4)=1−0.7=0.3
Therefore, the probability of e4 is:
P(e4)=0.3
The probability of e4 is 0.3.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - Matching The Columns2videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PROBABILITYEXERCISE - True/False7videos
PROBABILITY
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTION EXERCISE - OBJECTIVE TYPE QUESTIONS5videos
PRINCIPLE OF MATHEMATICAL INDUCTION
- BOOK - NCERT EXEMPLAR ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - True /False5videos
RELATIONS AND FUNCTIONS
Similar Questions
If P(E)=0.05, what is the probability of not E?
View SolutionIf P(E)=0.25, What is the probability of not E.
View SolutionIf P(E)=0.08, What is the probability of not E.
View SolutionIf E1 and E2 be two events such that P(E1)=0.3,P(E2)=0.2 and P(E1∩E2)=0.1, then find:
(i) P(¯¯¯E1∩E2) (ii) P(E1∩¯¯¯E2)View SolutionIf E1 and E2 are two events such that P(E1)=1/4, P(E2/E1)=1/2 and P(E1/E2)=1/4, then
View SolutionLet E1andE2 be two independent events such that P(E1)=P1 and P(E2)=P2, describe in words of the events whose probabilities are
(i) P1P2 (ii) (1−P1)P2
(iii) 1−(1−P1)(1−P2) (iv) P1+P2−2P1P2View SolutionSuppose that E1 and E2 are two events of a random experiment such that P(E1)=14,P(E2∣E1)=12andP(E1∣E2)=14. Observe the lists given below :
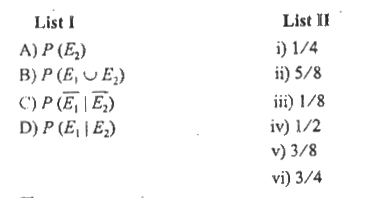
The correct matching of the list I from the list II is :View SolutionABCD is a rhombus with AC=2BD. Diagonals AC and BD intersect at P.E1,E2,E3andE4 are four ellipes passing through P and their foci are A and B, B and C, C and D and D and A, respectively . If for i=1,2,3,4,ei are the eccentricities fo Ei, then
View SolutionIf e1ande2 are the eccentricities of the ellipse x218+y24=1 and the hyperbola x29−y24=1 respectively and (e1,e2) is a point on the ellipse 15x2+3y2=k, then the value of k is equal to
View SolutionOf the three independent event E1,E2 and E3, the probability that only E1 occurs is α, only E2 occurs is β and only E3 occurs is γ. If the probavvility p that none of events E1,E2 or E3 occurs satisfy the equations (α−2β)p=αβ and (β−3γ)p=2βγ. All the given probabilities are assumed to lie in the interval (0, 1). Then, probability of occurrence of E1probability of occurrence of E3 is equal to
View Solution

