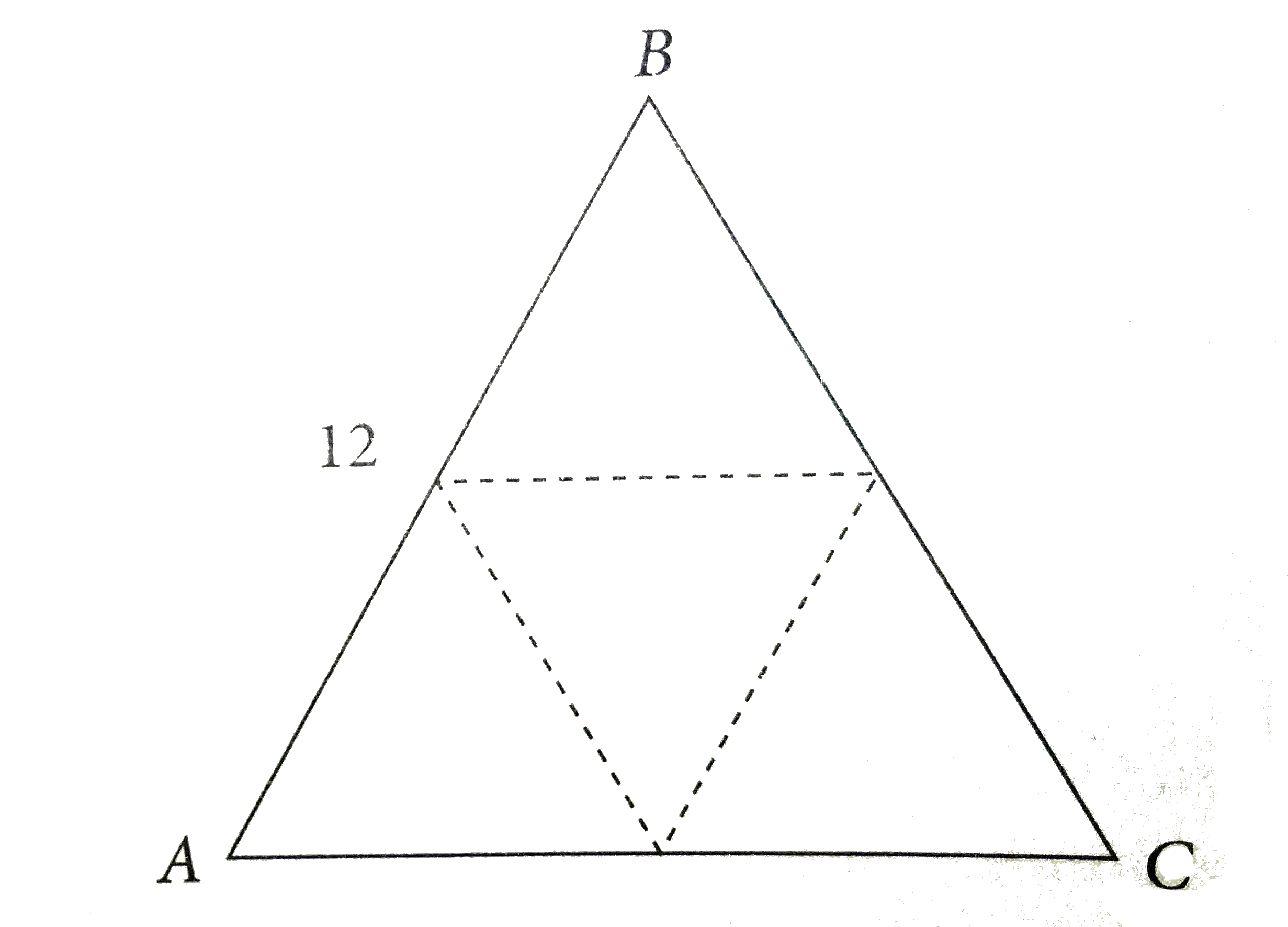
If equilibrium triangle ABC is cut by three lines , as shows , to form four equilibrium triangles of equal area , what is the length of a side of one of the smaller triangles?
3
4
5
6
The correct Answer is:D
Step by step video, text & image solution for If equilibrium triangle ABC is cut by three lines , as shows , to form four equilibrium triangles of equal area , what is the length of a side of one of the smaller triangles? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 12: CIRCLES, QUADRILATERALS, AND VOLUME
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 13: ADVANCED GEOMETRY
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 10: LINES, ANGLES, AND COORDINATES
11 Videos
- PRACTICE TEST 4BOOK - PRINCETONCHAPTER - PRACTICE TEST 4EXERCISE - Math Test-Calculator
38 Videos
- SAT MATH: THE BIG PICTUREBOOK - PRINCETONCHAPTER - SAT MATH: THE BIG PICTUREEXERCISE - Example
4 Videos
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2In the figure, what is the area of ΔABC?
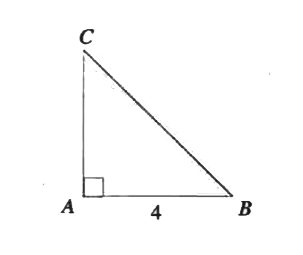 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenAD is the longest side of the triangle ABD shown in the figure. What is the length side of ΔABC ?
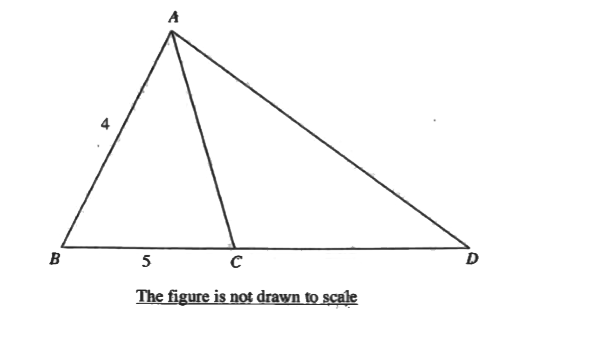 A2B3C√41D9
A2B3C√41D9
At equilibrium ,ΔG=……………
View SolutionThe areas of two similar triangles are 169 cm2 and 121 cm2 respectively. If the longest side of the larger triangle is 26cm, what is the length of the longest side of the smaller triangle?
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionShow that the diagonals of a parallelogram divide it into four triangles of equal area.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View Solution