If the area of triangle ABC is 15, what is the length of AC ?
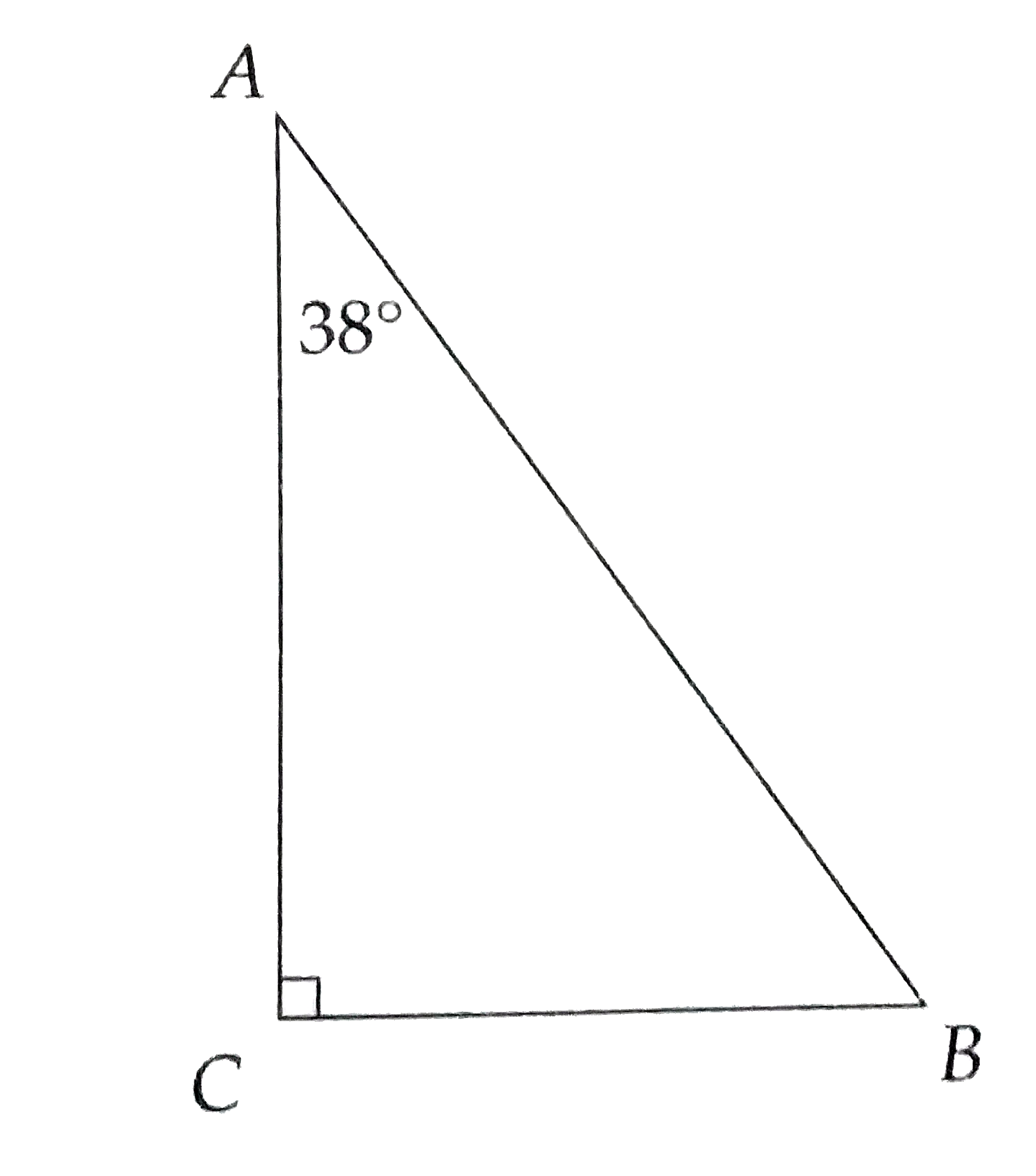
2.1
4.1
6.2
8.2
The correct Answer is:C
Use the given angle to find the ratio of the legs :
BCAC=tan38∘≈0.781
If you call AC (the leg you're looking for) x, then you can call leg BC 0.781 x. Half the product of the legs is the area, or 15 :
Area =12(leg1)(leg2)
15=12(x)(0.781x)
0.781x2=30
x2=300.781≈38.4
x≈6.2
Topper's Solved these Questions
Similar Questions
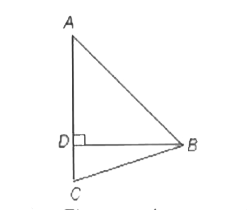
Triangle ABC has the same area as a rectangle with sides of lengths 5 and 7. If the length of ¯¯¯¯¯¯AC is 10, what is the length of ¯¯¯¯¯¯BD?View SolutionTriangle ABC is inscribed in a circle, such that AC is a diameter of the circle and angle BAC is 45∘. If the area of triangle ABC is 72 square units, how larger is the area of the circle than the area of triangle ABC ?
View Solution
Knowledge Check
- Question 1 - Select One
If the area of △ABC is 21, and the length of the height minus the length of the base equals 1, which of the following is equal to the base of the triangle ?
A2B4C6D7 - Question 2 - Select One
The average length of the sides of ΔABC is 12. What is the perimeter of ΔABC?
 A4B6C12D36
A4B6C12D36 - Question 3 - Select One
In the figure, ABCD is a rectangle, and the area of ΔACE is 10. What is the area of the rectangle?
 A18B22.5C36D44
A18B22.5C36D44

In ΔABC what is the length of ¯¯¯A?View SolutionLet ABC be an equilateral triangle, let KLMN be a rectangle with K, L on BC , M on AC and N on AB. Suppose AN/NB=2 and the area of triangle BKN is 6. The area of the triangle ABC is -
View SolutionIn triangle ABC, the measure of ∠B is 90∘, BC = 16, and AC = 20. Triangle DEF is similar to triangle ABC, where vertices D, E, and F correspond to vertices A, B, and C, respectively, and each side of triangle DEF is 13 the length of the corresponding side of triangle ABC. What is the value of sin F ?
View SolutionGiven a triangle ABC with AB=2 and AC=1. Internal bisector of ∠BAC intersects BC at D. If AD = BD and Δ is the area of triangle ABC, then find the value of 12Δ2.
View SolutionIn Fig. 3, the area of triangle ABC (in sq. units) is :
View Solution

