If f(x)= maximum {x3,x2,164}∀x∈[0,∞) then
A
f(x)={x2,0≤x≤1x3,x>1
B
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩164,0≤x≤14x2,14<x≤1x3,x>1
C
f(x)=⎧⎪ ⎪ ⎪⎨⎪ ⎪ ⎪⎩164,0≤x≤18x2,18<x≤1x3,x>1
D
f(x)={164,0≤x≤18x3,x>1/8
Video Solution
Text Solution
The correct Answer is:C
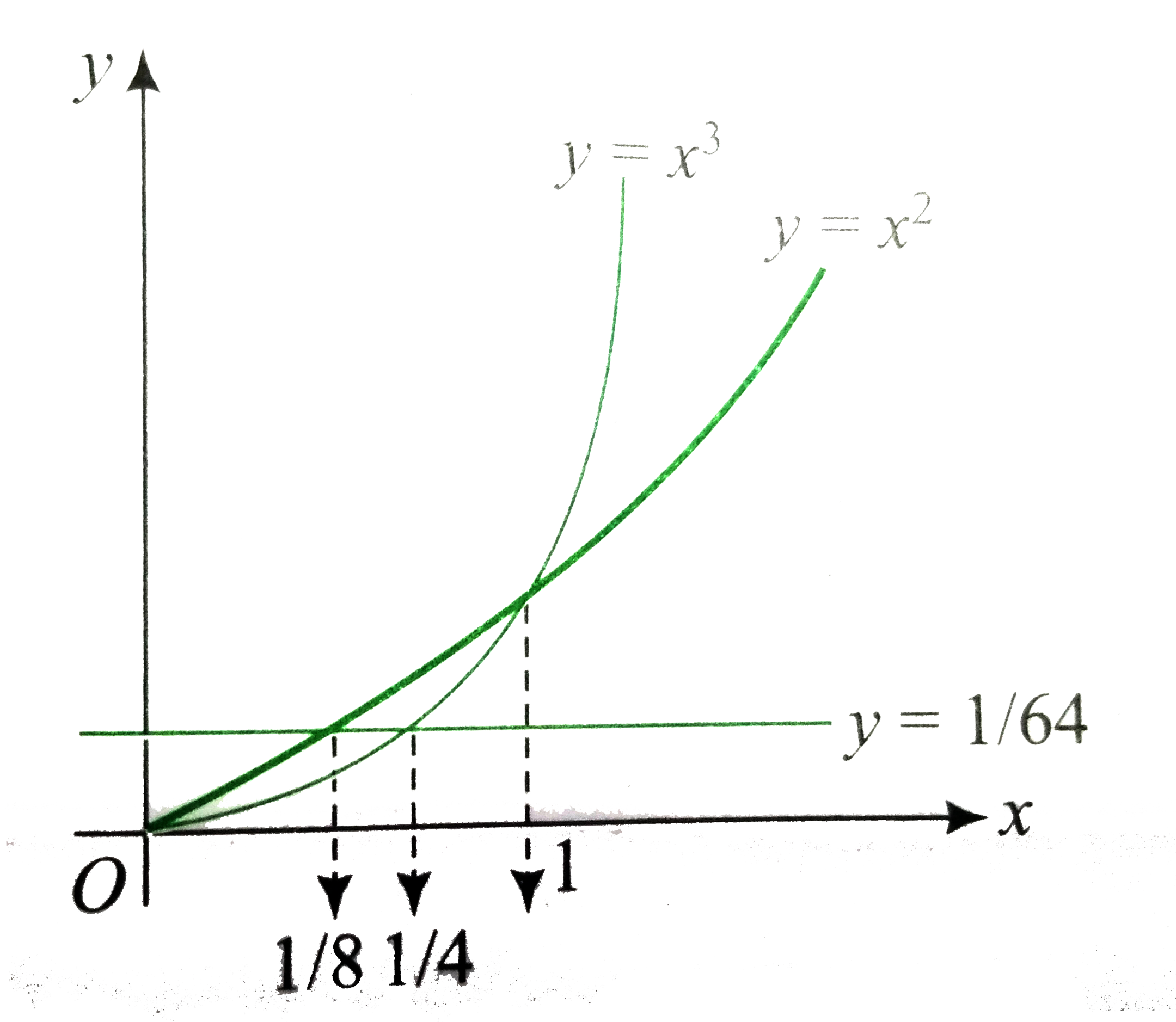
Clearly, from the graph, f(x)=⎧⎪
⎪
⎪⎨⎪
⎪
⎪⎩164,0≤x≤18x2,18<x≤1x3,x>1
|
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Multiple)
27 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.15
8 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
31 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Knowledge Check
Consider a function f(x)=xx,∀x∈[1,∞). If g(x) is the inverse function of f(x), then the value of g'(4) is equal to
Alog2eB12log2eeC14log2eeD12log22eLet f(x)<0∀x∈(≡∞,0)andf(x)>0∀x∈(0,∞) also f(0)=o, Again f'(x)<0∀x∈(−∞,−1)andf'(x)>∀x∈(−1,∞) also f'(−1)=0 given limx→∞f(x)=0andlimx→∞f(x)=∞ and function is twice differentiable.
If f'(x)<0∀x∈(0,∞)andf'(0)=1 then number of solutions of equatin f(x)=x2 is :A1B2C3D4Let f(x) be differentiable ∀x. If f(1)=-2 and f'(x)≥2∀x∈x[1,6], then:
Af[6]<5Bf[6]=5Cf[6]≥8Df(6)<8
if f(x)=max{x2,x3,164} for all x∈(0,∞)
View SolutionDiscuss the differentiability of f(x)=maξμm{2sinx,1−cosx}∀x∈(0,π).
View SolutionIf f(x)=x1+(Inx)(lnx)...∞∀x∈[1.∞) then ∫2e1f(x)dx equals:
View SolutionIf f(x)={2x2+2x2∀x∈[−2,2]−{0}.Then the sum of global maximum and global minimum of f(x) is
View SolutionThe function f(x) satisfy the equation f(1−x)+2f(x)=3x∀x∈R, then f(0)=
View Solution
