If f(x)=xe[x]+|x|−2[x]+|x|, then limx→0f(x) is.
A
-1
B
0
C
1
D
non-existent
Video Solution
Text Solution
The correct Answer is:D
We have,
limx→0−f=(x)limx→0−xe−1−x−2−1−x[∵[x]=−1and|x|=−x for−1<x<0]
⇒limx→0−f(x)=0×e−1−2−1=0
and , limx→0+f(x)=limx→0x(e−x−2x)[∵[x]=0and|x|=xfor−1<x<0]
⇒limx→0+f(x)=limx→0ex−2=1−2=−1
∴limx→0f(x) does not exist.
|
Updated on:21/07/2023
Related Playlists
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section I - Solved Mcqs101videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section II - Assertion Reason Type5videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test30videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise30videos
MATHEMATICAL INDUCTION
Similar Questions
If f(x)=sin(ex−2−)log(x−1) then limx→2f(x) is given by
View SolutionEvaluate limx→0f(x), where
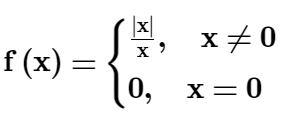 View Solution
View SolutionIf f(x)=|x|x, then show that limx→0f(x) does not exist.
View SolutionIf f(x)=tanxx−π, then limx→(π)f(x)=……………….
View SolutionIf y(x)=|x|−3,findlimx→3f(x).
View SolutionIf f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
View SolutionIf limx→0[1+x+f(x)x]1/x=e3, then limx→0[1+f(x)x]1/x=
View SolutionLet f(x)={|x|x,x≠00,x=0.
Find limx→0f(x).View SolutionIf f(x)=∣∣ ∣ ∣∣sinxcosxtanxx3x2x2x1x∣∣ ∣ ∣∣, then limx→0f(x)x2 is equal to
View Solutionf(x)=ex then limx→0f(f(x))1f(x) is
View Solution


