If f(x)=√(1+px)−√(1−px)x , −1≤x<0
=2x+1x−2 , 0≤x≤1
is continuous in the interval [−1,1] .
Find P.Solution in Malayalam
Step by step video & image solution for If f(x)=(sqrt((1+px))-sqrt((1-px)))/x , -1lex<0 =(2x+1)/(x-2) , 0lexle1 is continuous in the interval [-1,1] . Find P. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
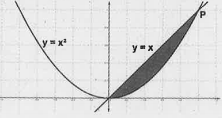
Consider the following figure
find the point of intersection (P) of the parabola and the line.
 04:28View Solution
04:28View SolutionUsing properties of determinants prove
∣∣ ∣ ∣∣xyx+yyx+yxx+yxy∣∣ ∣ ∣∣=−2(x3+y3)02:40View Solutionf(x)={√1+px−√1−pxx,−1≤x<02x+1x−2,0≥x≥1 is continuous in the interval [−1,1], then p is equal to −1 (b) −12 (c) 12 (d) 1
03:31View Solutionf(x)={[(srt(1+px)-sqrt(1-px))/x,-1<=x<0],[(2x+1)/(x-2),0<=x<=1]}is continuous in the interval [-1, 1], then 'p' is equal to:,0
04:46View Solutionint(p(x^(p)-1))/(x^(p+1)sqrt(1-2x^(p)+px^(2p)))dx=
02:36View Solutionयदि f(x)=⎧⎨⎩√1+px−√1−pxx,−1≤x<02x+1x−1,0≤x≤1
अंतराल [−1,1] में सतत हो, तो सिद्ध कीजिये p=−106:17View SolutionIf f(x)=⎧⎨⎩√1+px−√1−pxx,−1≤x<02x+1x−2,0≤x≤1 is continuous in [-1,1] then p is equal to
03:28View Solutionf(x)=⎧⎨⎩√1+px−√1−pxx,यदि−1≤x<02x+1x−2,यदि−0≤x≤1
06:17View SolutionIf f(x) =√1+px−√1−pxx, if −12≤x<0=3x2+2x−2, if 0≤x<1 is continuous on its domain , then : p =
View Solutionमाना कि f(x)=⎧⎨⎩√1+px−√1−pxxयदि−1≤x<02x+1x−2यदि0≤x<1
p के किस मान के लिए फलन f(x) सतत होगा?04:18View SolutionIf f(x)=⎧⎨⎩√1+px−√1−pxx,−1≤x<02x+1x−20≤x≤1 is continues on [−1,1] then p=
03:36View SolutionIf f(x)=⎧⎨⎩√1+px−√1−pxx,−1≤x<02x+1x−2,0≤x≤1
continauous on [ -1,1], then p =View Solutionf(x) = (sqrt(1+px) - sqrt(1 - px))/(x), -1 le x le 0 = (2x + 1)/(x-2), 0 le x le 1 is continuous in the interval [-1, 1], then p is :
06:05View SolutionIf p∈(−1,1) , then roots of the quadratic equation (p−1)x2+px+√1−p2=0 are
05:58View Solutionf(x)={√1+px−√1−pxx,−1≤x<02x+1x−2,0≥x≥1 is continuous in the interval [−1,1], then p is equal to −1 (b) −12 (c) 12 (d) 1
05:47View Solutionf(x)={√1+px−√1−pxx,−1≤x<02x+1x−2,0≥x≥1 is continuous in the interval [−1,1], then p is equal to −1 (b) −12 (c) 12 (d) 1
06:04View Solution

