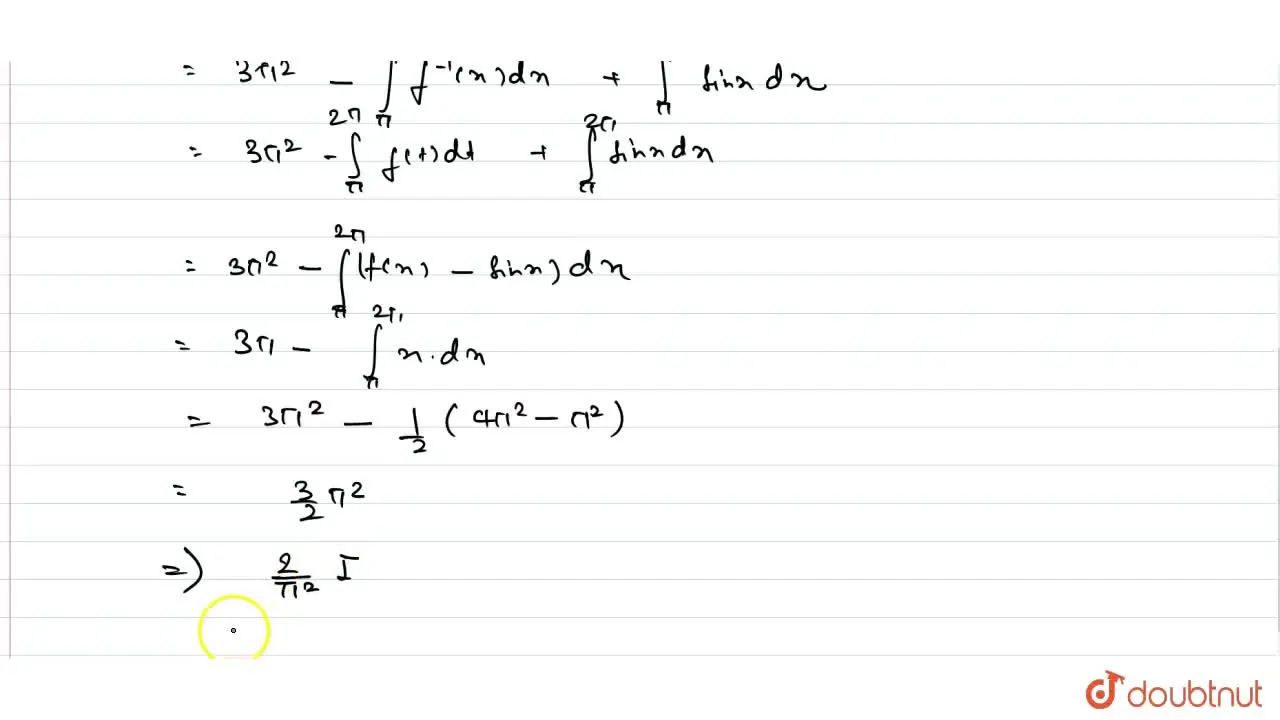if f(x)=x+sinx, then find 2π2.∫2ππ(f−1(x)+sinx)dx
Video Solution
Text Solution
The correct Answer is:3
Let x=f(t)⇒dx=f′(t)dt
⇒∫2πxf−1(x)dx=∫2ππtf′(t)dt=(t[f(t)])2ππ−unt2ππf(t)dt
=(4π2−π2)−∫2ππf(t)dt
I=∫2ππf(t)dt+∫2ππsinxdx=3π2−∫2ππf−1(x)dx+∫2ππsinxdx
=3π2−∫2ππf(t)dt+∫2ππsinxdx=3π2−∫2ππ(f(x)−sinx)dx
=3π−∫2ππx.dx=3π2−12(4π2−π2)=32π2⇒2π2I=3
|
Updated on:21/07/2023
Related Playlists
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS SEC - 11videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - PART : 1MATHEMATICS9videos
TEST PAPERS
- BOOK - RESONANCECHAPTER - TEST PAPEREXERCISE - CHEMISTRY37videos
TEST PAPER
- BOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - MATHEMATICS131videos
TEST SERIES
Similar Questions
If f(x)=x+sinx, then find the value of ∫2ππf−1(x)dx.
View Solution∫π0x1+sinxdx.
View Solution∫π2−π2[[x]+sinx]dx=?
View SolutionIf f:R→R defined by f(x)=sinx+x, then find the value of ∫π0(f−1(x))dx
View SolutionIf f(x)=sinx−x,then ∫2π−2π∣∣f−1(x)∣∣dx= (A) π2 (B) 2π2 (C) 3π2 (D) 4π2
View SolutionIf f(x)=1−cosx1−sinx, then: f'(π2) is
View Solution∫π20cos2xcosx+sinxdx=
View SolutionIf fx=x+sinx, then ∫2ππf−1(x)dx is equal to
View Solution∫π2−π21+sin2x1+πsinxdx=
View Solution∫π20sinx1+cos2xdx
View Solution