If f(x)={xsin(1x)x≠00x=0 Then, limx→0f(x)
is equal to 1
is equal to−1
is equal to 0
does not exist
The correct Answer is:C
Step by step video, text & image solution for If f(x)={(xsin,((1)/(x)),xne0),(0,,x=0):} Then, lim_(xrarr0) f(x) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Chapter Test60videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - LIMITSEXERCISE - Section II - Assertion Reason Type5videos
LIMITS
- BOOK - OBJECTIVE RD SHARMACHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test30videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - OBJECTIVE RD SHARMACHAPTER - MATHEMATICAL INDUCTION EXERCISE - Exercise30videos
MATHEMATICAL INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
f(x)={|x|cos(1x)x≠00x=0 is
Adiscontinuous at x=0Bcontinuous at x=0Cdoes not existDNone of the above - Question 2 - Select One
f(x)={(2−Sin(1x))|x|x≠00x=0
AMonotonic in (−∞,0)∪(0,∞)BNot Monotonic in (−∞,0)∪(0,∞)CMonotonic in (−∞,∞)DNot Monotonic in (−∞,∞)
Let f(x)={|x|x,x≠02,x=0.
Show that limx→0f(x) does not exist.View SolutionLet f(x)={3x|x|+2x'x≠00,x=0.
Show that limx→0f(x) does not exist.View SolutionIf f(x)={xnsin(1x2)x≠00x=0, (n∈I), then (a) limx→0f(x) exists for n>1 (b) limx→0f(x) exists for n<0 (c) limx→0f(x) does not exist for any value of n (d) limx→0f(x) cannot be determined
View SolutionIf f(x)={x−|x|x,x≠02, x=0,show that limx→0f(x) does not exist.
View SolutionIf f(x) is defined as follows:
f(x)⎧⎪⎨⎪⎩1x>0−1x<00x=0
Then show that limx→0f(x) does not exist.View SolutionEvaluate limx→0f(x), where
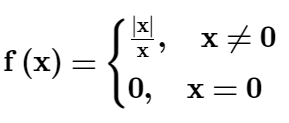 View Solution
View Solution

