
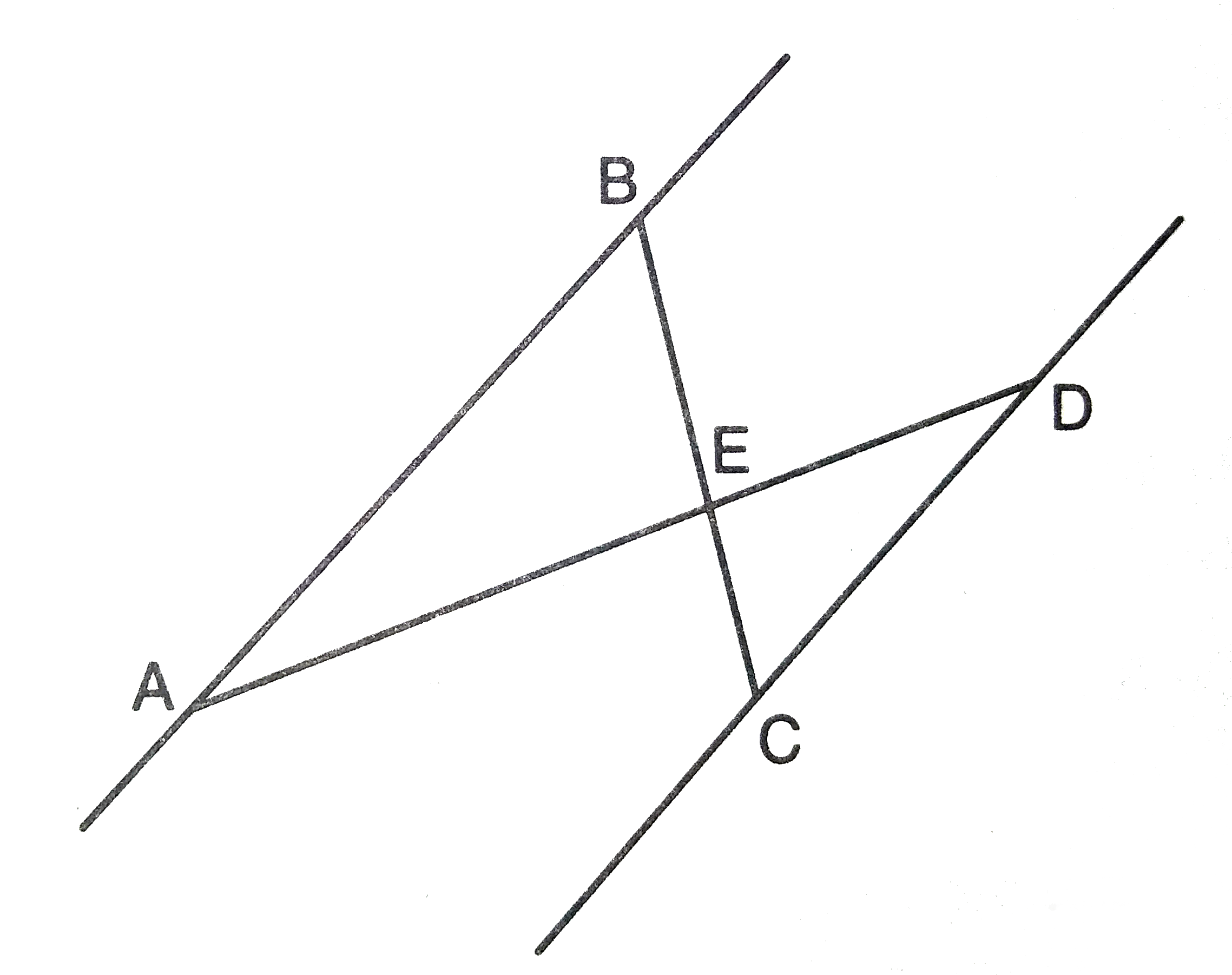
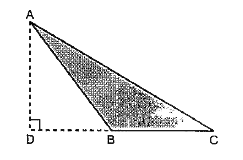
If, in the figure above, CD=1, AB=-2, and AD=6, then BC=
5
9
2+√5
3√5
The correct Answer is:D
Step by step video, text & image solution for If, in the figure above, CD=1, AB=-2, and AD=6, then BC= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - Grib-In
32 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATHBOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATHEXERCISE - EXERCISE
45 Videos
- ADDITIONAL TOPICS IN MATH BOOK - ENGLISH SATCHAPTER - ADDITIONAL TOPICS IN MATH EXERCISE - PRACTICE TEST
24 Videos
- COMPLEX NUMBERSBOOK - ENGLISH SATCHAPTER - COMPLEX NUMBERSEXERCISE - EXERCISE
6 Videos
Similar Questions
in the given figure ∠CAB=90∘andAD⊥BC. if AC= 75 cm , AB= 1m and BD= 1.25 m . Find AD.

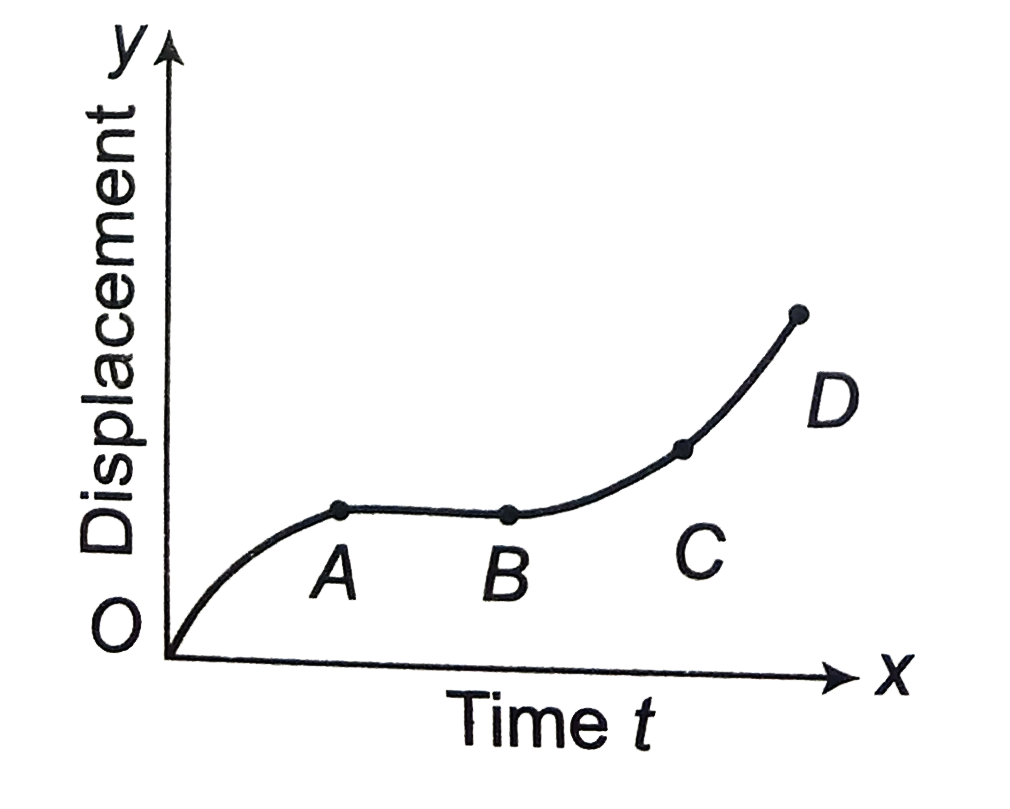
View SolutionThe graph between the displacement x and time t for a particle moving in a straight line is shown in the figure. During the interval OA,AB,BC and CD the acceleration of the particle is
OA,AB,BC,CD
View Solution
Knowledge Check
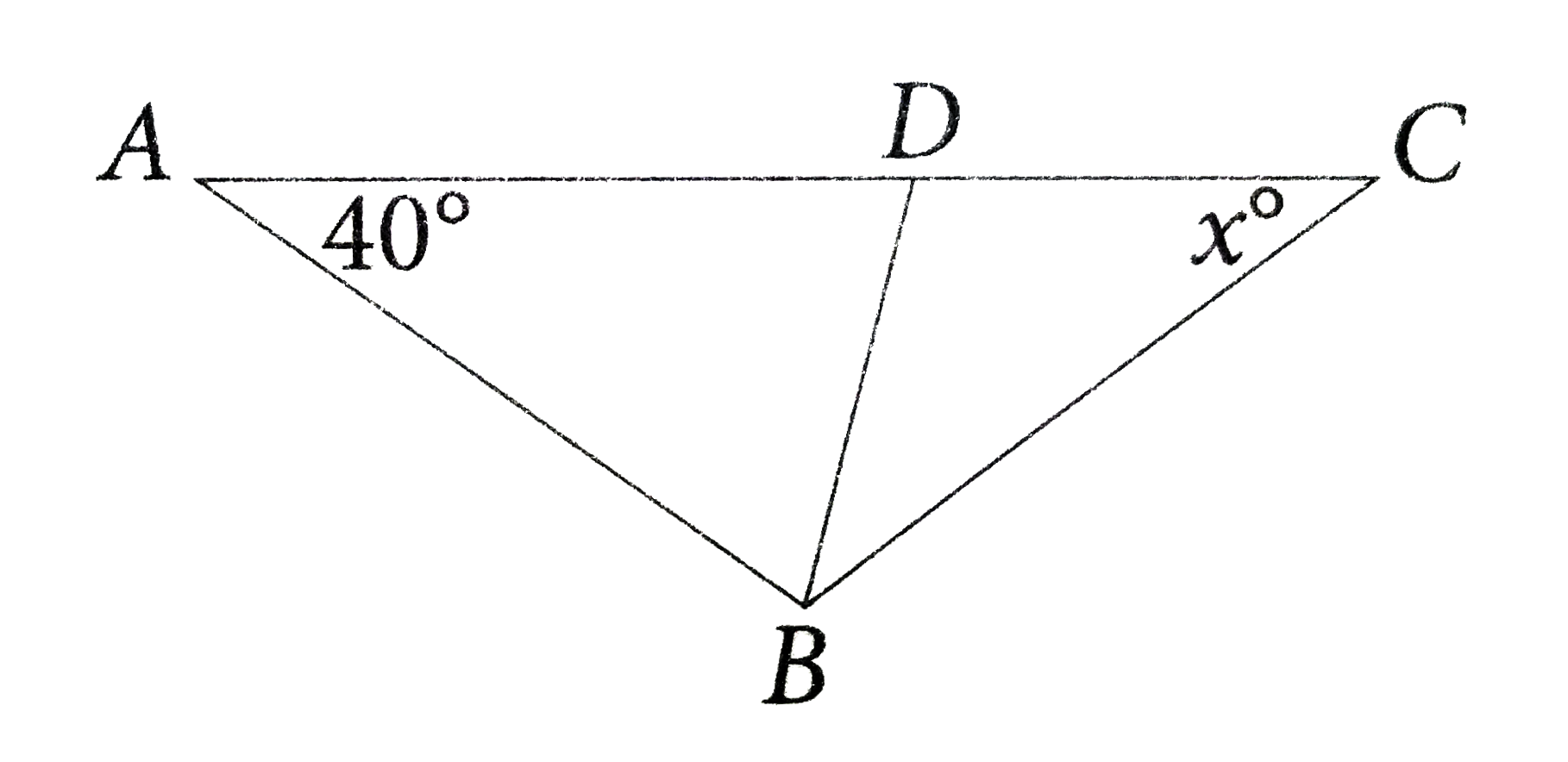
In the figure above, DB=DC and AB=AD. What is the value of x?A110B70C55D35In the figure, if AB=8,BC=6,AC=10andCD=9, then AD =
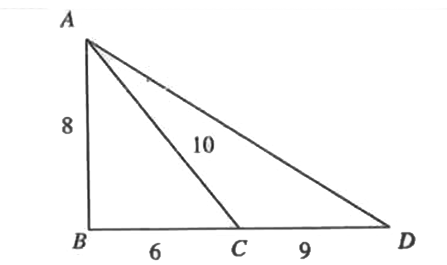 A12B13C15D17
A12B13C15D17In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD, AD=42, AB=12, and CD=16, what is the length of ¯¯¯¯¯¯DE?
A21B24C27D30
In the figure above, ¯¯¯¯¯¯AB∣∣¯¯¯¯¯¯CD, AD=30, AB=21, and CD=15. What is the length of ¯¯¯¯¯¯DE?
View SolutionABCD is a trapezium such that AB and CD are parallel and BC⊥CD. If ∠ADB=θ,BC=pandCD=q, then AB is equal to
View SolutionIn the given figure, AB∣∣CD,AB=7cm,BD=25cmandCD=17cm, find the length of side BC.

View SolutionIn a kite shaped figure ABCD , AB = AD and CB = CD , point P,Q and r are mid-point of sides AB,BC and CD respectively . Prove that:
( i) ∠PQR=90∘
(ii) Line through P and parallel to QR bisects side AD.
View SolutionIn the figure AB = BC and AD is perpendicular to CD. Prove that :
AC2=2.BC.DC
View Solution
