If limx→a(f(x)g(x)) exists, then
limx→c f(x) exist
neither limx→c f(x) nor limx→c g(x) may exist
limx→c g(x) exist
both limx→c f(x) and limx→c g(x) must exist
The correct Answer is:B
Step by step video, text & image solution for If lim_(x->a)(f(x)/(g(x))) exists, then by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITS AND CONTINUITYBOOK - MCGROW HILL PUBLICATIONCHAPTER - LIMITS AND CONTINUITYEXERCISE - Questions for Previous Years AIEEE/JEE Main Papers
44 Videos
- JEE (MAIN) QUESTIONS WITH SOLUTIONS MATHEMATICS (7 TH JAN-MORNING )BOOK - MCGROW HILL PUBLICATIONCHAPTER - JEE (MAIN) QUESTIONS WITH SOLUTIONS MATHEMATICS (7 TH JAN-MORNING )EXERCISE - QUESTIONS
25 Videos
- MATHEMATICAL INDUCTION AND BINOMIAL THEOREMBOOK - MCGROW HILL PUBLICATIONCHAPTER - MATHEMATICAL INDUCTION AND BINOMIAL THEOREMEXERCISE - Questions from Previous Years. B-Architecture Entrance Examination Papers
20 Videos
Similar Questions
Knowledge Check
If limx→a[f(x)g(x)] exists, then which one of the following correct ?
ABoth limx→af(x)andlimx→ag(x) must existBlimx→af(x) need not exist but limx→ag(x) must existCBoth limx→af(x)andlimx→ag(x) need not existDlimx→af(x) must exist but limx→ag(x) need not existConsider the following statements :
1. If limx→af(x)andlimx→ag(x) both exist, then limx→a{f(x)g(x)} exists.
2. If limx→a{f(x)g(x)} exists, then both limx→af(x)andlimx→ag(x) must exist.
Which of the above statements is /are correct?A1 onlyB2 onlyCBoth 1 and 2DNeither 1 nor 2verify the statement true or false.If limx→a[f(x)g(x)] exists, then both limx→af(x)andlimx→ag(x) exist.
AOnly 1BOnly 2CBoth 1 and 2DNeither 1 nor 2
verify the statement true or false.If limx→a[f(x)g(x)] exists, then both limx→af(x)andlimx→ag(x) exist.
View Solution1.if limx→af(x) and limx→ag(x) both exist , then limx→a{f(x)g(x)} exists. 2. If limx→a{f(x)g(x)} exists, then both limx→af(x) and limx→ag(x) exist. Which of the above statements is/are correct ?
View SolutionWhich of the statement(s) is/are incorrect? (A) If f+ g is continuous at x = a, then f and g are continuous at x= a (B) If limx→a(fg)∃,then⊥hlim_x->a f and lim_(x->a) g exist. (C) Discontinuity at x = a means non-existence of limit. (D) All functions defined on a closed interval attain a maximum or a minimum value in that interval.
View Solution. If limx→cf(x)−f(c)x−c exists finitely, then1) limf(x) = f(c) 2) limf (x) = f(c)3) limf(x) does not exist4) limf(x) may or may not exist
View Solutionlet
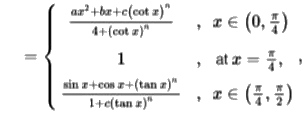 where a, b, c are real constants and f(x)=limn→∞g(x). If
where a, b, c are real constants and f(x)=limn→∞g(x). If
limx→π4 f(x) exists, then c may be x→π4 equal to
View Solution
