If O is the origin and if the coordinates of any two points Q1 and Q2 are (x1,y1) and (x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.Solution in Bengali
Step by step video & image solution for If O is the origin and if the coordinates of any two points Q_1 \ a n d \ Q_2 are (x_1,y_1) \ a n d \ (x_2,y_2), respectively, prove that O Q_1.O Q_2cos/_Q_1O Q_2=x_1x_2+y_1y_2. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Let z1 and z2 be two distinct complex numbers and z=(1−t)z1+tz2, for some real number t with 0<t<1 and i=√−1. If arg(w) denotes the principal argument of a non-zero compolex number w, then
03:06View SolutionFind x where f(x)=max{√x(2−x),2−x} is non-differentiable.
03:05View SolutionThe coordinates of two points PandQ are (x1,y1)and(x2,y2)andO is the origin. If the circles are described on OPandOQ as diameters, then the length of their common chord is |x1y2+x2y1|PQ (b) |x1y2−x2y1|PQ |x1x2+y1y2|PQ (d) |x1x2−y1y2|PQ
02:27View SolutionLet A and B have coordinates (x_1,y_1) and (x_2,y_2) respectively. We define the distance between A and B as d(A,B) =max||x_2-x_1|,|y_2-y_1|| If d(A,O)=1 where O is the origin then locus of A has an area of
05:02View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
02:36View SolutionIf θ is the angle which the straight line joining the points (x1,y1)and (x2,y2) subtends at the origin, prove that tanθ=x2y1−x1y2x1x2+y1y2 andcosθ=x1x2+y1y2√x12+y12x22+y22
03:04View SolutionThe electric force on a charge q1 due to q2 is (4ˆi−3ˆj)N. What is the force on q2 due to q1?
View SolutionIn previous question the ratio of heat flow at M and N are Q_1 and Q_2 respectively. Then –
03:33View SolutionIf the coordinates of any two points Q1andQ2 are (x1,y1) and (x2,y2), respectively, then prove that OQ1×OQ2cos(∠Q1OQ2)=x1x−2+y−1y2, whose O is the origin.
04:04View Solution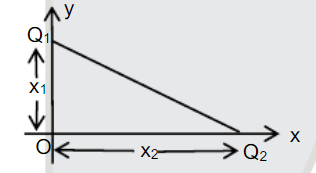
Two charge Q1 and Q2 are placed in xy plane at a distance x1 and x2 from origin a shown in figure. if electric field at O is same for both charge then find ratio Q1 and Q2.04:24View SolutionIf O is the origin and if the coordinates of any two points Q1 and Q2 are (x1,y1) and (x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.
02:08View SolutionThe coordinates of two points PandQ are (x1,y1)and(x2,y2)andO is the origin. If the circles are described on OPandOQ as diameters, then the length of their common chord is (a)|x1y2+x2y1|PQ (b) |x1y2−x2y1|PQ |x1x2+y1y2|PQ (d) |x1x2−y1y2|PQ
04:00View SolutionIf the coordinates of any two points Q1andQ2 are (x1,y1) and (x2,y2), respectively, then prove that OQ1×OQ2cos(∠Q1OQ2)=x1x−2+y−1y2, whose O is the origin.
07:23View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
01:35View SolutionIf θ is the angle which the straight line joining the points (x1,y1)and (x2,y2) subtends at the origin, prove that tanθ=x2y1−x1y2x1x2+y1y2 andcosθ=x1x2+y1y2√x12x22+y22x12+y12x22+y12y22
01:59View SolutionTwo charge Q_1 and Q_2 are placed in xy plane at a distance x_1 and x_2 from origin a shown in figure. if electric field at O is same for both charge then find ratio Q_1 and Q_2 .
07:06View Solution

