If the coordinates of any two points Q1andQ2 are (x1,y1) and (x2,y2), respectively, then prove that OQ1×OQ2cos(∠Q1OQ2)=x1x−2+y−1y2, whose O is the origin.
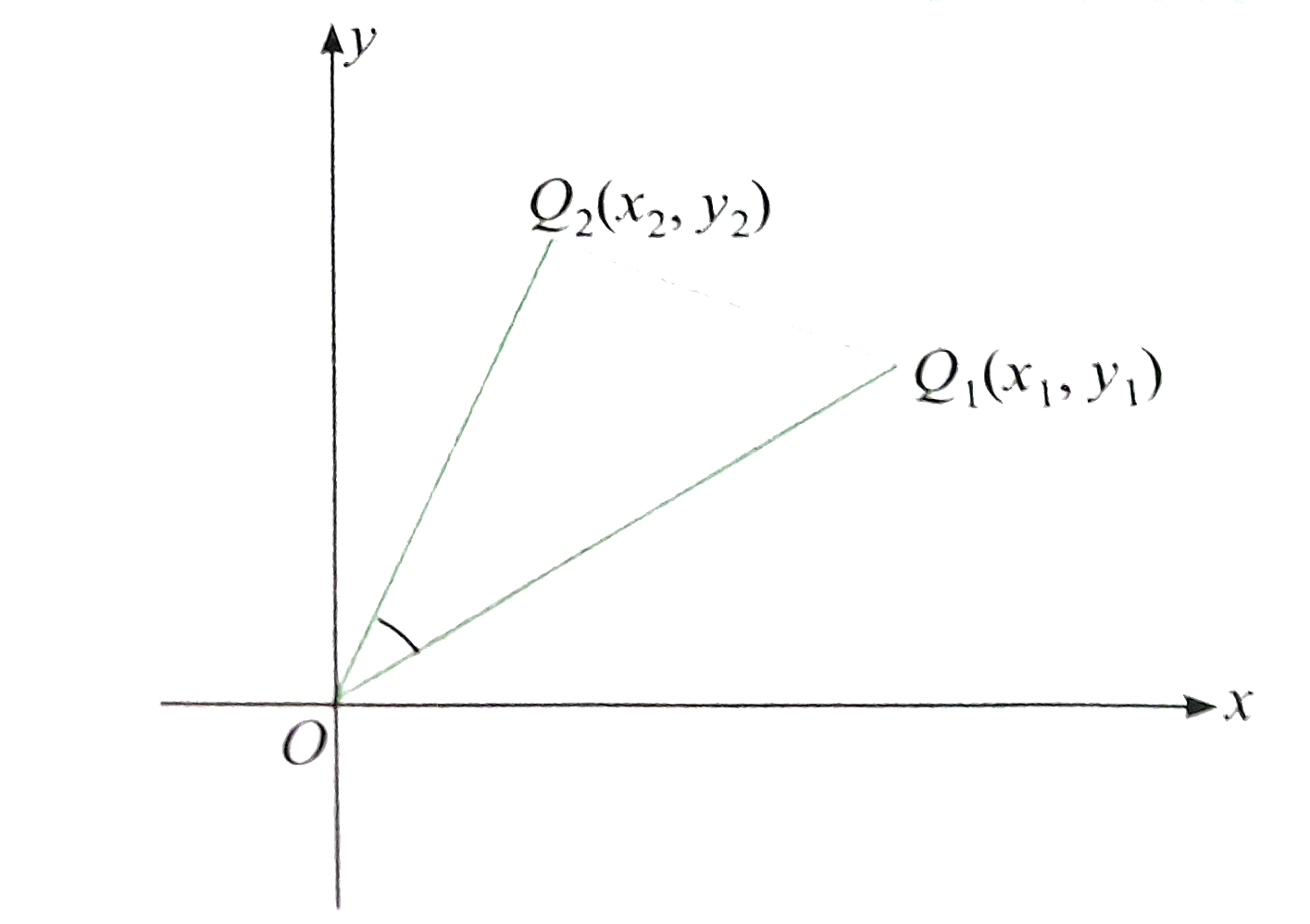
In ΔOQ1Q2, using cosing rule, we get
(Q−1Q2)2=(OQ1)2+(OQ2)2−OQ1.OQ2.cos(∠Q1OQ2)
∴(x2−x1)2+(y2−y1)2
=(x21+y21)+(x22+y22)−2OQ1.OQ2.cos(∠Q1OQ2)
⇒OQ1.OQ2cos(∠Q1OQ2)=x1x2+y1y2.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If O is the origin and if the coordinates of any two points Q1andQ2 are (x1,y1)and(x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.
View SolutionIf O is the origin and if the coordinates of any two points Q1 and Q2 are (x1,y1) and (x2,y2), respectively, prove that OQ1.OQ2cos∠Q1OQ2=x1x2+y1y2.
View Solution
Knowledge Check
If O be the origin and Q1(x1,y1) and Q2(x2,y2) be two points then OQ1.OQ2cos(∠Q1OQ2) is equal to
Ax1y2+x2y1B(x21+y21)(x22+y22)C(x1−x2)2+(y1−y2)2Dx1x2+y1y2If the point x1+t(x2−x1),y1+t(y2−y1) divides the join of (x1,y1) and (x2,y2) internally then
At<0B0<t<1Ct>1Dt=1
If O be the origin, and if the coordinates of any two points P1, and P2, be respectively (x1,y1) and (x2,y2), prove that: OP1.OP2.cosP1OP2=x1.x2+y1.y2.
View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
View SolutionIf the line segment joining the points P(x1,y1)and Q(x2,y2) subtends an angle α at the origin O, prove that : OP.OQ cosα=x1x2+y1y2.
View SolutionIf [x−y2x−x12x−y3x+y1],=[−15013] and coordinats of points P and Q be (x,y) and (x1,y1) respectively then P,Q=?
View SolutionIf [x−y2x−x12x−y3x+y1],=[−15013] and coordinats of points P and Q be (x,y) and (x1,y1) respectively then P,Q=?
View SolutionThe coordinates of the ends of a focal chord of the parabola y2=4ax are (x1,y1) and (x2,y2) . Then find the value of x1x2+y1y2 .
View Solution
