If seven slips of paper are labelled as 1, 2, 3, 4, 6, 7, 8 and one slip is drawn out of it, then what is the probability that it is
(i) a 7 ?
(ii) greater than 4?
(iii) an odd number?
iiiiii1/73/74/7
iiiiii1/73/73/7
iiiiii1/72/75/7
iiiiii1/75/72/7
The correct Answer is:B
To solve the problem, we need to determine the probability for three different scenarios based on the slips of paper labeled 1, 2, 3, 4, 6, 7, and 8.
Total Outcomes:
The total number of slips is 7, which are labeled as follows:
1, 2, 3, 4, 6, 7, 8
(i) Probability of drawing a 7:
1. Identify the favorable outcome: The only favorable outcome for this event is the slip labeled '7'.
2. Count the favorable outcomes: There is 1 favorable outcome (the slip labeled '7').
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=17
(ii) Probability of drawing a number greater than 4:
1. Identify the favorable outcomes: The numbers greater than 4 from the slips are 6, 7, and 8.
2. Count the favorable outcomes: There are 3 favorable outcomes (6, 7, 8).
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=37
(iii) Probability of drawing an odd number:
1. Identify the favorable outcomes: The odd numbers from the slips are 1, 3, and 7.
2. Count the favorable outcomes: There are 3 favorable outcomes (1, 3, 7).
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=37
Summary of Probabilities:
- (i) Probability of drawing a 7: 17
- (ii) Probability of drawing a number greater than 4: 37
- (iii) Probability of drawing an odd number: 37
The total number of slips is 7, which are labeled as follows:
1, 2, 3, 4, 6, 7, 8
1. Identify the favorable outcome: The only favorable outcome for this event is the slip labeled '7'.
2. Count the favorable outcomes: There is 1 favorable outcome (the slip labeled '7').
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=17
1. Identify the favorable outcomes: The numbers greater than 4 from the slips are 6, 7, and 8.
2. Count the favorable outcomes: There are 3 favorable outcomes (6, 7, 8).
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=37
1. Identify the favorable outcomes: The odd numbers from the slips are 1, 3, and 7.
2. Count the favorable outcomes: There are 3 favorable outcomes (1, 3, 7).
3. Calculate the probability:
Probability=Number of favorable outcomesTotal outcomes=37
- (i) Probability of drawing a 7: 17
- (ii) Probability of drawing a number greater than 4: 37
- (iii) Probability of drawing an odd number: 37
Topper's Solved these Questions
- IMO QUESTION PAPER 2019-20 SET-BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019-20 SET-BEXERCISE - Everyday Mathematics
10 Videos
- IMO QUESTION PAPER 2019-20 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019-20 SET AEXERCISE - Achievers Section
5 Videos
- IMO QUESTION PAPER 2020-21 SET-ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020-21 SET-AEXERCISE - ACHIEVERS SECTION
5 Videos
Similar Questions
In a throw of one dice the samle space S = { 1 , 2 , 3 , 4 , 5 , 6 } ⇒ n ( S ) = 6 (i) Let E 1 = event of getting 5 = { 5 } ⇒ n ( E 1 ) = 1 and P ( E 1 ) = n ( E 1 ) n ( S ) = 1 6 (ii) Let E 2 = event of getting a number greater than 2 = { 3 , 4 , 5 , 6 } ⇒ n ( E 2 ) = 4 P ( E 2 ) = n ( E 2 ) n ( S ) = 4 6 = 2 3 (iii) Let E 3 = event of getting 6 = { } ⇒ n ( E 3 ) = 0 ∴ P ( E 3 ) = n ( E 3 ) n ( S ) = 2 6 = 0 (iv) Let E 4 = event of getting and odd number = { 1 , 3 , 5 } ⇒ n ( E 4 ) = 3 ∴ P ( E 4 ) = n ( E 4 ) n ( S ) = 3 6 = 1 2
View SolutionA die is thrown. What is the probability of getting (i) a prime number?
(ii) a number greater than 4? (ii) a number not greater than 5?
View Solution
Knowledge Check
Seven digits from the numbers 1, 2, 3, 4, 5, 6, 7, 8 and 9 are written in random order. The probability that this seven digit number is divisible by 9 is :
Aa. 79Bb. 19Cc. 29!Dd. 49
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (see figure) and these are equally likely outcomes. What is the probability that it will point at :
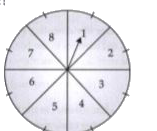
(i) 8? (ii) an odd number?
(iii) a number greater than 2? (iv) a number less 9?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2 3,4,5,6,7,8 and these are equally likely outcomes what is the probability that it will point at :
(i) 8?
(ii) an odd number ?
(iii) a number greater than 2 ?
(iv) a number less than 9 ?
View SolutionA die is rolled once.Find the probability of getting: (i) an odd number (iii) number greater than 0
View SolutionIn a single throw of two dice what is the probability of obtaining a number greater than 7 , if 4 appears on the first dice?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 (See Fig. 131), and these are equally likely outcomes. What is the probability that it will point at (i) 8? (ii) an odd number? (iii) a number greater than 2? (iv) a number less than 9?
View SolutionA game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,1,8 (see Figure), and these are equally likely outcomes. What is the probability that it will point at(i) 8?(ii) an odd number?(iii) a number greater than 2?(iv) a number less than 9?
View SolutionThe letters written on paper slips of the word MEDIAN are put in a bag. If one slip is drawn randomly, what is the probability that it bears the letter D?
View Solution
