If 4∑i−1(ξ2+yi2)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are the vertices of a rectangle collinear the vertices of a trapezium none of theseSolution in Tamil
the vertices of a rectangle
collinear
the vertices of a trapezium
none of these
The correct Answer is:A
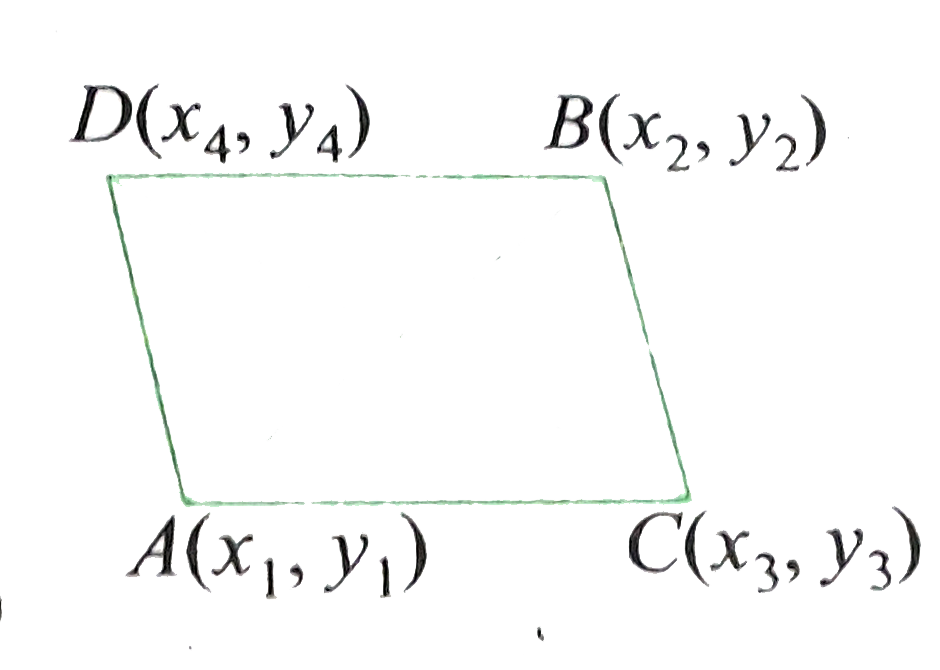
Let A≡(x1,y1),B≡(x2,y2),C≡(x3,y3),D≡(x4,y4)
Given
x21+x22+x24+y21+y22+y23+y24−2x1x3−2x2x4−2y2y3−2y1y4≤0
or (x1−x3)2+(x2−x4)2+(y2−y3)2+(y2−y3)2+(y1−y4)2≤0
or x1+x22=x3+x42andy1+y22=y4+y32
Hence AB and CD bisect each other. therefore, ACBD is a parallelogram. Also,
AB2=(x1−x2)2+(y1−y2)2
=(x3−x4)2+(y4−y3)2
=CD2
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionStudy the diagram. The line l is perpendicular to line m Does PE bisect CG?
View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionTheorem : The area of a triangle the coordinates of whose vertices are (x1;y1);(x2;y2)and(x3;y3) is 1/2|(x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)|
View SolutionIf the points (x1,y1),(x2,y2)and(x3,y3) be collinear, show that: y2−y3x2x3+y3−y1x3x2+y1−y2x1x2=0
View SolutionIf x1,x2,x3 as well as y1,y2,y3 are in A.P., then the points (x1,y1),(x2,y2),(x3,y3) are (A) concyclic (B) collinear (C) three vertices of a parallelogram (D) none of these
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy=c2 in four points P(x1,y1),Q(x2,y2),R(x3,y3),S(x4,y4), then : (A) x1+x2+x3+x4=0 (B) y1+y2+y3+y4=0 (C) x1x2x3x4=c4 (D) y1y2y3y4=c4
View Solutionif Σ4i=1(x2i+y2i)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are
View Solutionयदि तीन बिंदु (x1,y1),(x2,y2) तथा (x3,y3) संरेख है तो सिद्ध कीजिए की
(x3−x1)(y2−y1)=(x2−x1)(y3−y1)
View SolutionIf the normals at the four points (x1,y1),(x2,y2),(x3,y3)and(x4,y4) on the ellipse x2a2+y2b2=1 are concurrent. Prove that (x1+x2+x3+x4)((1x1+1x2+1x3+1x4)=4
View SolutionA triangle has vertices Ai(xi,yi)fori=1,2,3 If the orthocentre of triangle is (0,0), then prove that
∣x2−x3y2−y3y1(y2−y3)+x1(x2−x3)
x3−x1y2−y3y2(y3−y1)+x1(x3−x1)
x1−x2y2−y3y3(y1−y2)+x1(x1−x2)∣=0
View SolutionIf the points (x1,y1),(x2,y2), and (x3,y3) are collinear show that y2−y3x2x3+y3−y1x3x1+y1−y2x1x2=0
View SolutionIf 4∑i−1(x12+y12)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are the vertices of a rectangle collinear the vertices of a trapezium
View SolutionWrite the condition of collinearity of points (x1, y1), (x2, y2) and (x3, y3) .
View Solution
