if Σ4i=1(x2i+y2i)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are
the vertices of a rectangle
collinear
the vertices of a trapezium
none of these
The correct Answer is:A
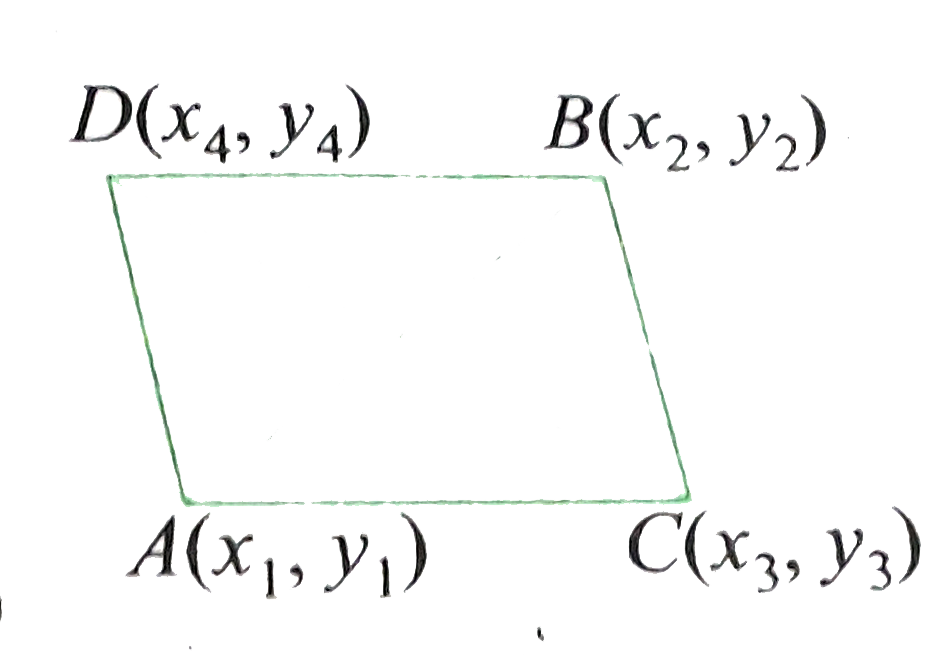
Let A≡(x1,y1),B≡(x2,y2),C≡(x3,y3),D≡(x4,y4)
Given
x21+x22+x24+y21+y22+y23+y24−2x1x3−2x2x4−2y2y3−2y1y4≤0
or (x1−x3)2+(x2−x4)2+(y2−y3)2+(y2−y3)2+(y1−y4)2≤0
or x1+x22=x3+x42andy1+y22=y4+y32
Hence AB and CD bisect each other. therefore, ACBD is a parallelogram. Also,
AB2=(x1−x2)2+(y1−y2)2
=(x3−x4)2+(y4−y3)2
=CD2
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Comprehension)
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If 4∑i−1(x12+y12)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are the vertices of a rectangle collinear the vertices of a trapezium
View SolutionIf 4∑i−1(ξ2+yi2)≤2x1x3+2x2x4+2y2y3+2y1y4, the points (x1,y1),(x2,y2),(x3,y3),(x4,y4) are the vertices of a rectangle collinear the vertices of a trapezium none of these
View Solution
Knowledge Check
(x1−x2)2+(y1−y2)2=a2
(x2−x3)2+(y2−y3)2=b2 and
(x3−x1)2+(y3−y1)2=c2 then
14∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣ is equal toAs(s−a)2B(s−b)(s−c)2Cs(s−a)(s−b)(s−c) wher 2s=a+b+cDnone
Four points (x1,y1),(x2,y2),(x3,y3)and(x4,y4) are such that 4∑i=1(x2i+y2i)≤2(x1x3+x2x4+y1y2+y3y4) Then these points are vertices of - (A) Parallelogram (B) Rectangle (C) Square (D) Rhombus
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy=c2 at four points P(x1,y1),Q(x2,y2),R(x3,y3), and S(x4,y4), then x1+x2+x3+x4=0 y1+y2+y3+y4=0 x1x2x3x4=C4 y1y2y3y4=C4
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy=c2 at four points P(x1,y1),Q(x2,y2),R(x3,y3), and S(x4,y4), then x1+x2+x3+x4=0 y1+y2+y3+y4=0 x1x2x3x4=C4 y1y2y3y4=C4
View SolutionIf the circle x2+y2=a2 intersects the hyperbola xy=c2 at four points P(x1,y1),Q(x2,y2),R(x3,y3), and S(x4,y4), then x1+x2+x3+x4=0 y1+y2+y3+y4=0 x1x2x3x4=C4 y1y2y3y4=C4
View SolutionIf the coordinates of the vertices of an equilateral triangle with sides of length a are (x1,y1),(x2,y2) and (x3,y3) then ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=3a44
View SolutionIf the coordinates of the vertices of an equilateral triangle with sides of length a are (x1,y1),(x2,y2) and (x3,y3) then ∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣2=3a44
View SolutionIf (x1−x2)2+(y1−y2)2=a2,(x2−x3)2+(y2−y3)2=b2and(x3−x1)2+(y3−y1)2=c2 then prove that 4∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣=(a+b+c)(b+c−a)(c+a−b)(a+b−c)
View Solution
