If the angle between two tangents drawn from an external point P to a circle of radius $a$ and center O , is $60^{\circ},$ then find the length of OP.

A

$2 a$

B

$4 a$

C

$6 a$

D

$8 a$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

PA and PB are two tangents from an external point P such that
$∠ A P B = 60^{\circ}$
$∴ ∠ O P A = ∠ O P B = 30^{\circ}$
( $∵$ tangents are equally inclined at the centre)
Also, $∠ O A P = 90^{\circ}$ (radius through point of contact is perpendicular to the tangent)

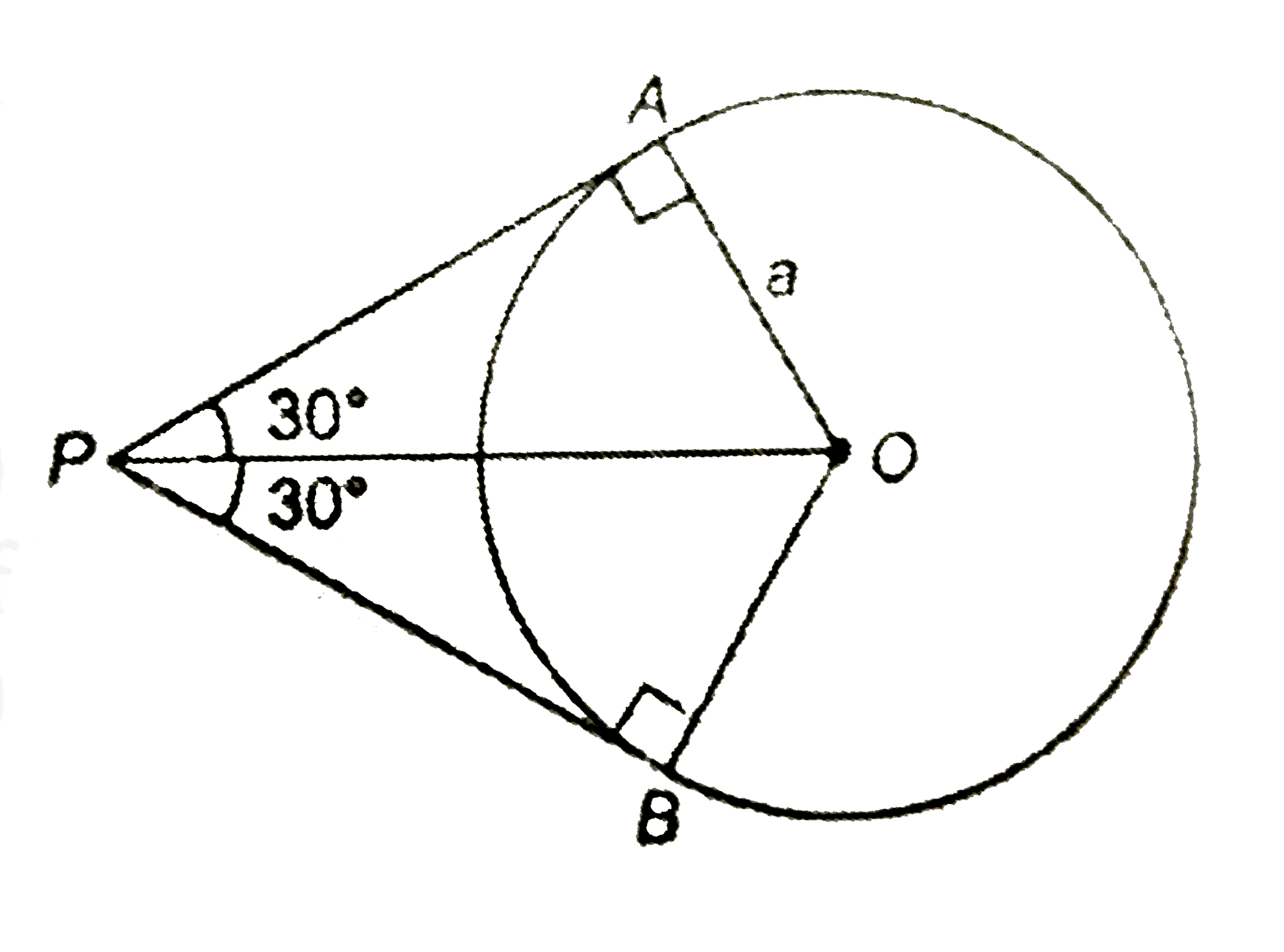
Now in right $Δ O A P,$
${sin 30}^{\circ} = \frac{O A}{O P}$
$\Rightarrow \frac{1}{2} = \frac{a}{O P} \Rightarrow O P = 2 a$ units

|

Updated on:21/07/2023

Class 10 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Write true or false and state reason
If angle between two tangents drawn from a point P to a circle of radius a and centre 0 is $90^{\circ}$ then $O P = a \sqrt{2}$ .
Atrue
Bfalse
Ccan not determine
Dnone of these

NAGEEN PRAKASHAN-CIRCLES-Revision Exercise Long Answer Questions

Home
Ask Doubt
Profile