If angle between two tangents drawn from a point P to a circle of radius 'a' and the centre O is 90∘ then prove that OP=√a
Step by step video & image solution for If angle between two tangents drawn from a point P to a circle of radius 'a' and the centre O is 90^@ then prove that OP=sqrt(a) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Similar Questions
यदि O केन्द्र और a त्रिज्या के वृत्त पर बाह्य बिन्दु P से खींची गई दो स्पर्श रेखाओं के मध्य कोण 60∘ है, तो OP की लम्बाई ज्ञात कीजिए।
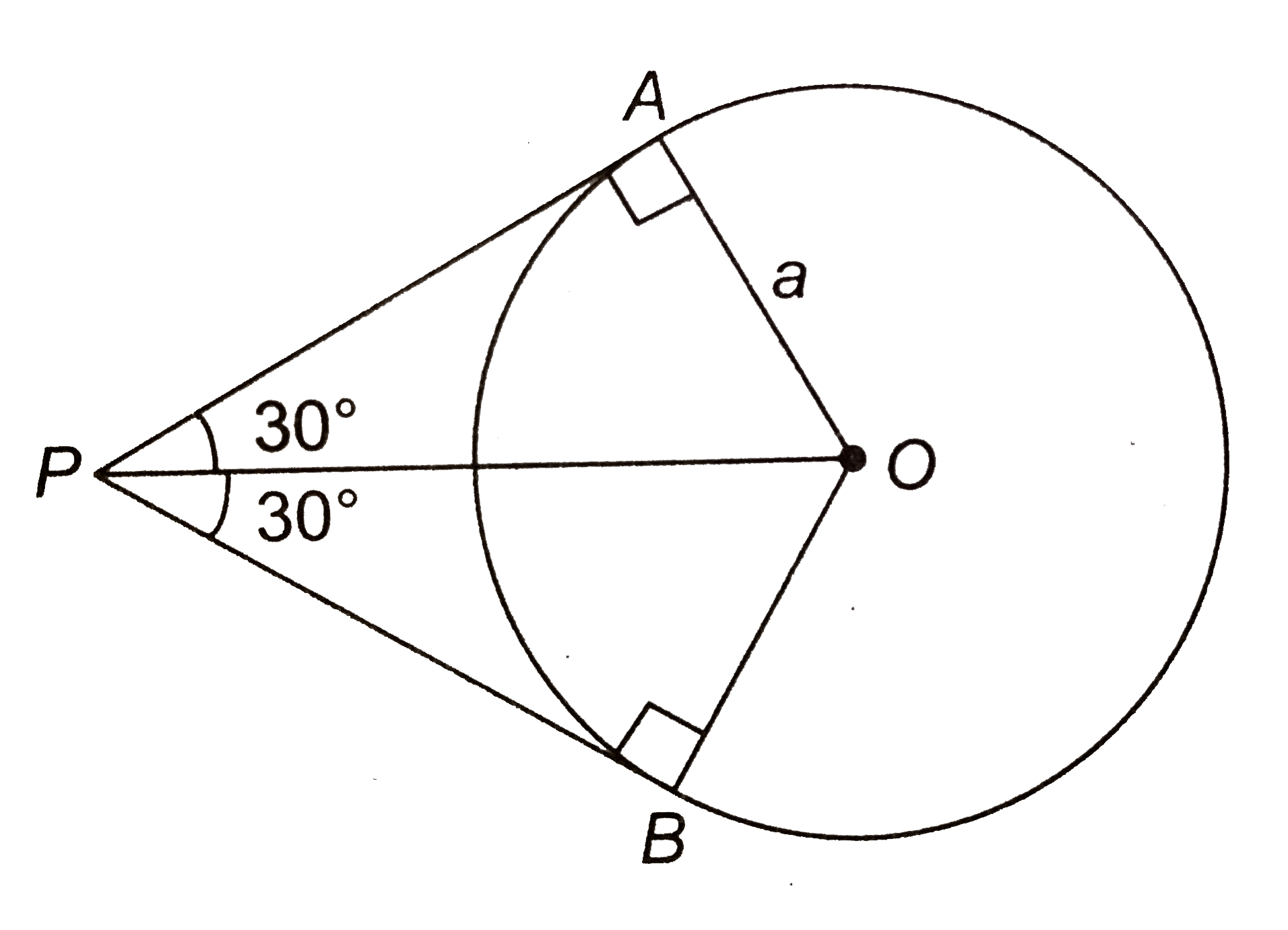 02:44View Solution
02:44View SolutionIf the angle between tangents drawn from a point P to a circle with radius a and center O 60^(@) If, find the length of OP.
02:44View SolutionWrite true or false and state reason:
If angle between two tangents drawn from a point P to a circle of radius a and centre O is 90∘ then OP=a√2.04:12View SolutionIf the angle between two tangents drawn from an external point ‘P’ to a circle of radius ‘r’ and centre O is 60∘, then find the length of OP.
05:08View SolutionP is a point in the plane of a circle with centre O and radius 4 cm. If OP = 3 cm, ..... tangent/s can be drawn to the circle from point P.
01:15View Solutionयदि किसी बिंदु P से त्रिज्या a और केंद्र O वाले वृत्त पर खींची गई स्पर्श रेखाओं के बीच का कोण 90∘ है, तो OP=a√2 होता है।
03:04View SolutionIf the angle between two tangents drawn from an external point P to a circle of radius 'a' and centre O, is 60∘, then find the length of OP.
03:02View SolutionFrom a point P, two tangents PA and PB are drawn to a circle with centre O. If OP is equal to diameter of the circle, then ∠APBis
03:27View Solution

