If the angle of elevation of a cloud from a point h metres above a lake is $α$ and the angle of depression of its reflection in the take is $β$ , prove that the height of the cloud is $(h \frac{tan β + t a n α}{tan β - t a n α}$

Video Solution

Text Solution

Verified by Experts

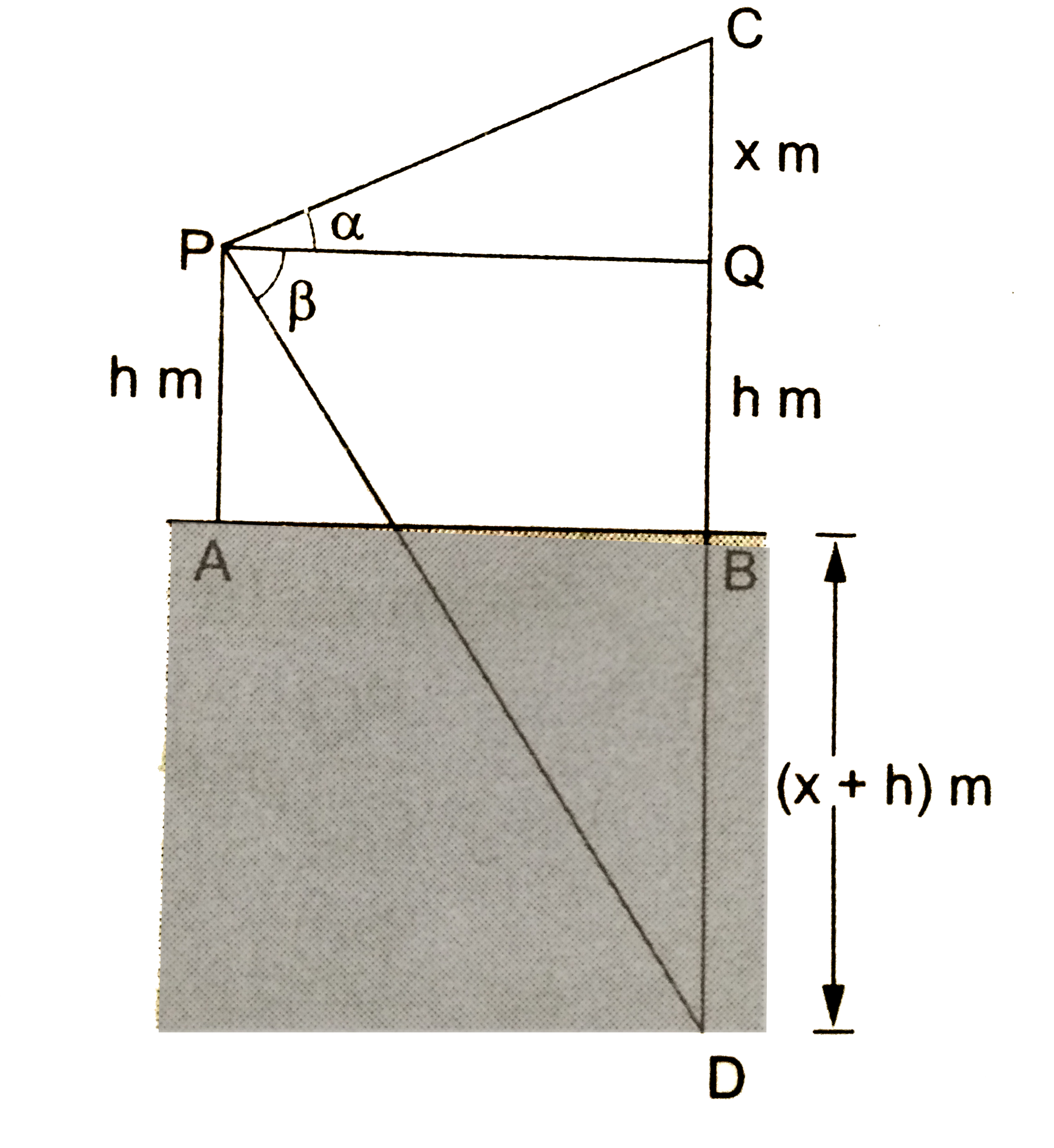
Let AB be the surface of the lake the let P be a point vertically above A such that $A P = h$ metres.
Let C be the position of the cloud and let D be its reflection in the lake.
Draw $P Q ⊥ C D$ . Then,
$∠ Q P C = α, ∠ Q P D = β$ ,
$B Q = A P = h$ metres.
Let $C Q = x$ metres. Then,
$B D = B C = (x + h)$ metres.
From right $Δ P Q C$ we have
$\frac{P Q}{C Q} = cot α \Rightarrow \frac{P Q}{x m} = cot α$
$\Rightarrow P Q = x cot α$ metres. $........... (i)$
From right $Δ P Q D$ , we have
$\frac{P Q}{Q D} = cot β \Rightarrow \frac{P Q}{(x + 2 h) m} = cot β$
$\Rightarrow P Q = (x + 2 h) cot β$ metres.
$\Rightarrow x (cot α - cot β) = 2 h cot β \Rightarrow x (\frac{1}{tan α} - \frac{1}{tan β}) = \frac{2 h}{tan β}$
$\Rightarrow x (\frac{tan β - tan α}{tan α + tan β}) = \frac{2 h}{tan β} \Rightarrow x = \frac{2 h tan α}{(tan β - tan α)}$
$∴$ height of the cloud from the surface of the lake
$= (x + h) = {\frac{2 h tan α}{(tan β + tan α)} + h} m$
$= \frac{h (tan α + tan β)}{(tan β - tan α)}$ metres.

Updated on:21/07/2023

|

Class 10 MATHS SOME APPLICATIONS OF TRIGONOMETRY

Topper's Solved these Questions

Similar Questions

Knowledge Check

If the angle of elevation of a cloud from a point 200m above a lake is $30^{\circ}$ and the angle of depression of its reflection in the lake is $60^{\circ}$ .Then the height of the cloud above the lake is :
A100 m
B200 m
C300 m
D400 m

RS AGGARWAL-HEIGHTS AND DISTANCES-Multiple Choice Questions (Mcq)

Home
Ask Doubt
Profile