If the angles subtended by two chords of a circle at the centre are equal, then Prove chords are equal.
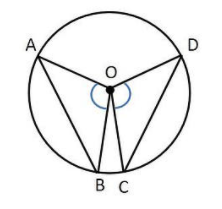
In △AOB and △DOC
OA=OD (radius)
∠AOB=∠DOC (given)
OB=OC (Radius)
By SAS congruency, △AOB and △DOC are congruent.
AB=CD (CPCT).
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.3
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.4
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.1
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
If the angles subtended by two chords of congruent circles at the corresponding centres are equal, then Prove chords are equal.
View SolutionTwo chords AB and CD intersect at P inside the circle . Prove that the sum of the angles substended by the arcs AC and BD at the centre O is equal to twice the angle APC.
View SolutionThe line joining the mid-points of two chords of a circle passes through its centre. Prove that the chords are parallel.
View SolutionChords of a circle which are equidistant from the centre are equal.
View SolutionIf angle subtended by any chord of a rectangular hyperbola at the centre is α and angle between the tangents at ends of chord is β, then
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionIf two arcs of a circle (or of congruent circles) are congruent, then corresponding chords are equal.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View SolutionA chord of a circle is equal to the radius of the circle find the angle subtended by the chord at a point on the monor arc and also at a point on the major arc.
View Solution
