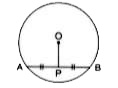
(Converse of Theorem 3) The line joining the centre of a circle to the mid-point of a chord is perpendicular to the chord.

In △AOX and △BOX
OA=OB (radius)
OX=OX (Common)
AX=BX (given)
By SSS congruency, △AOX and △BOX are congruent.
∠AXO=∠BXO (CPCT)
'
In line AB,
∠AXO+∠BXO=180
2∠AXO=180
∠AXO=∠BXO=90
Thus, OX⊥AB
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.5
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.6
1 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.3
1 Videos
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Knowledge Check
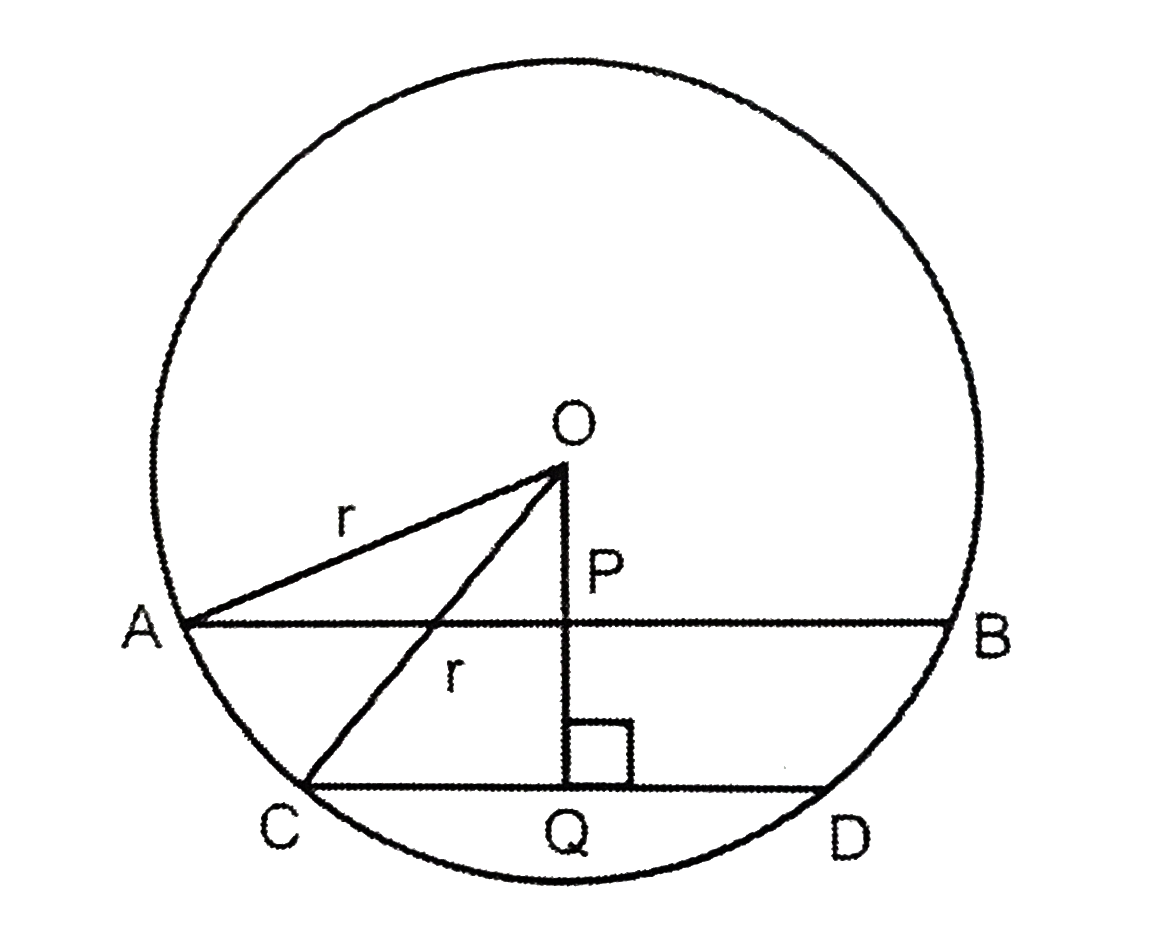
2 parallel chords 24 cm, and 18 cm, are on the same side of the centre of a circle. If the distance between the chords is 3 cm, calculate the radius of the circle.A15 cmB14 cmC13 cmD12 cm
The perpendicular from the centre of a circle to a chord bisects the chord.
View SolutionProve that the line joining the mid-point of a chord to the centre of the circle passes through the mid-point of the corresponding minor arc.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that : the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionIf two equal chords of a circle in intersect within the circle, prove that: the segments of the chord are equal to the corresponding segments of the other chord. the line joining the point of intersection to the centre makes equal angles with the chords.
View SolutionDescribe :
The locus of the mid-points of all chords parallel to a given chord of a circle.
View SolutionFind the locus of the centre of the circle passing through the vertex and the mid-points of perpendicular chords from the vertex of the parabola y2=4ax .
View SolutionProve that the line joining the mid-points of two parallel chords of a circle passes through the centre.
View Solution