If the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.Solution in Bengali
The correct Answer is:8 sq. units
The area of ellipse (x2/a2)+(y2/b2)=1isπab=4π (given) . Therefore, ab=4
A(acosθ,bsinθ)
on the ellipse.
Now, the area of reactangle ABCD inscribed in the ellipse is
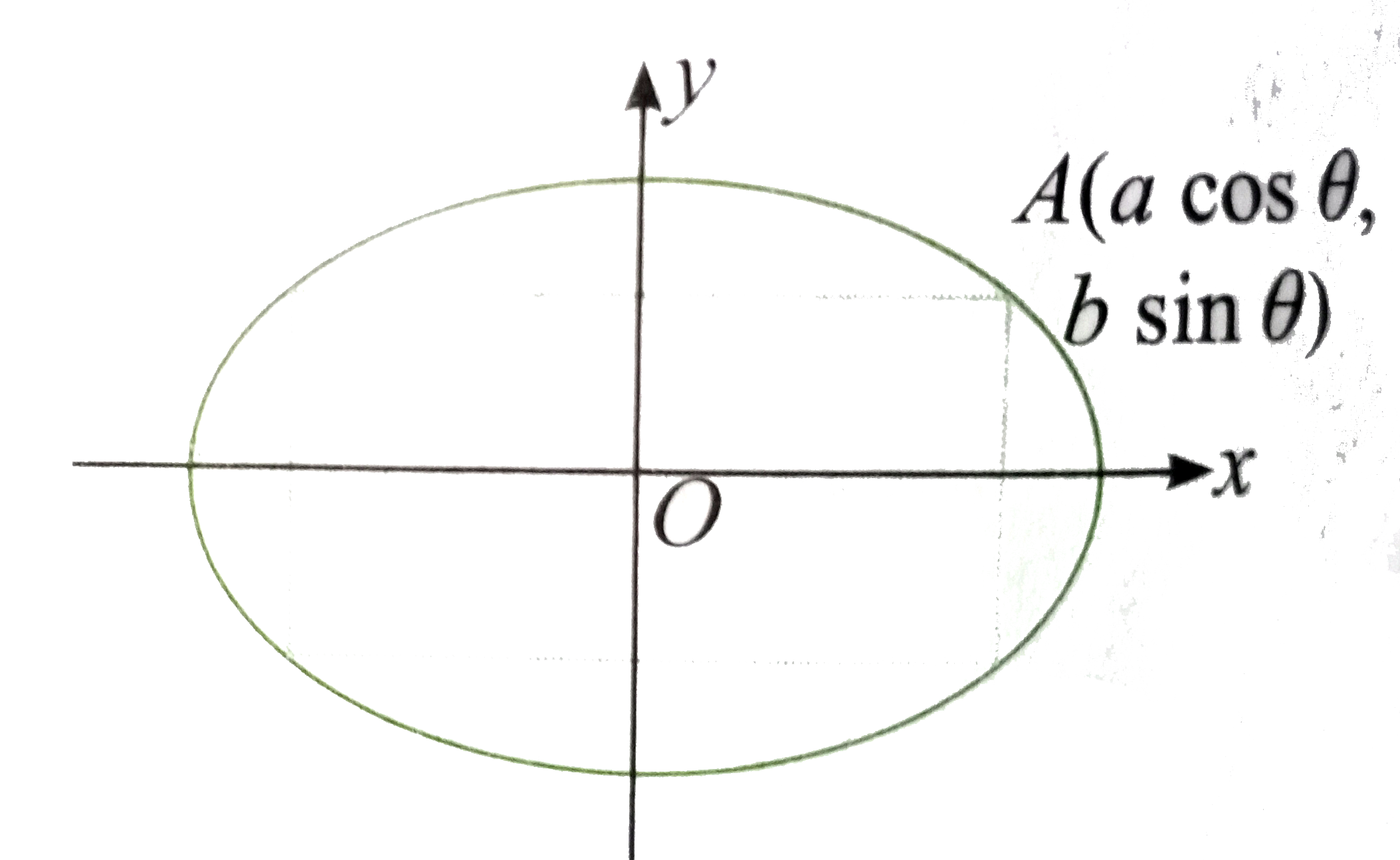
Δ=4(acosθ)(bsinθ)
or Δ=2|∈|2θ
∴Δmax=2ab=8
Similar Questions
Find the area of the greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionThe area of the rectangle of maximum area inscribed in the ellipse x225+y216=1 is
View SolutionFind the area of the greatest rectangle that can be inscribed in the ellipse (x^2)/(a^2)+(y^2)/(b^2)=1.
View SolutionIf the area of the ellipse (x2a2)+(y2b2)=1 is 4π , then find the maximum area of rectangle inscribed in the ellipse.
View SolutionFind the area of greatest rectangle that can be inscribed in an ellipse x2a2+y2b2=1.
View SolutionFind the area of the greatest rectangle that can be inscribed in an ellipse (x^2)/(a^2)+(y^2)/(b^2)=1 .
View Solution
