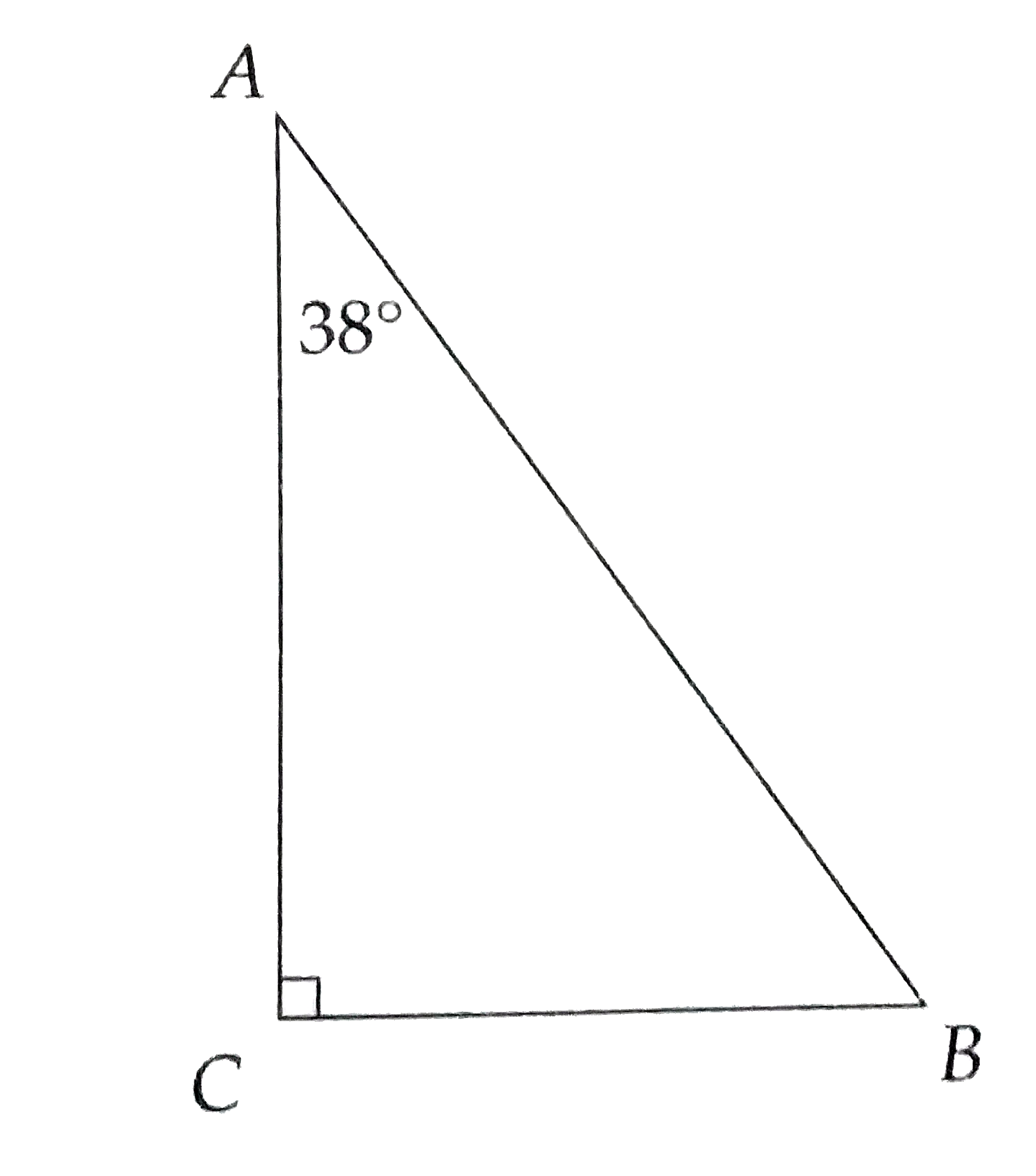
If the area of △ABC is 21, and the length of the height minus the length of the base equals 1, which of the following is equal to the base of the triangle ?
2
4
6
7
The correct Answer is:C
To solve the problem step by step, we will use the information provided in the question regarding the area of triangle ABC and the relationship between the height and the base.
Step 1: Define Variables
Let the base of the triangle be denoted as B and the height as H.
Step 2: Use the Area Formula
The area A of a triangle is given by the formula:
A=12×base×height
Given that the area is 21, we can write:
12×B×H=21
Multiplying both sides by 2 gives:
B×H=42(Equation 1)
Step 3: Use the Relationship Between Height and Base
We are also given that the height minus the base equals 1:
H−B=1
From this, we can express H in terms of B:
H=B+1(Equation 2)
Step 4: Substitute Equation 2 into Equation 1
Now, substitute H from Equation 2 into Equation 1:
B×(B+1)=42
Expanding this gives:
B2+B=42
Step 5: Rearrange the Equation
Rearranging the equation leads to:
B2+B−42=0
Step 6: Factor the Quadratic Equation
Next, we will factor the quadratic equation:
B2+7B−6B−42=0
Grouping the terms gives:
(B2+7B)+(−6B−42)=0
Factoring by grouping:
B(B+7)−6(B+7)=0
Factoring out (B+7):
(B+7)(B−6)=0
Step 7: Solve for B
Setting each factor to zero gives:
B+7=0orB−6=0
Thus, we find:
B=−7orB=6
Step 8: Determine the Valid Base Length
Since the length of the base cannot be negative, we discard B=−7 and accept:
B=6
Conclusion
The base of the triangle is 6.
Let the base of the triangle be denoted as B and the height as H.
The area A of a triangle is given by the formula:
A=12×base×height
Given that the area is 21, we can write:
12×B×H=21
Multiplying both sides by 2 gives:
B×H=42(Equation 1)
We are also given that the height minus the base equals 1:
H−B=1
From this, we can express H in terms of B:
H=B+1(Equation 2)
Now, substitute H from Equation 2 into Equation 1:
B×(B+1)=42
Expanding this gives:
B2+B=42
Rearranging the equation leads to:
B2+B−42=0
Next, we will factor the quadratic equation:
B2+7B−6B−42=0
Grouping the terms gives:
(B2+7B)+(−6B−42)=0
Factoring by grouping:
B(B+7)−6(B+7)=0
Factoring out (B+7):
(B+7)(B−6)=0
Setting each factor to zero gives:
B+7=0orB−6=0
Thus, we find:
B=−7orB=6
Since the length of the base cannot be negative, we discard B=−7 and accept:
B=6
The base of the triangle is 6.
Topper's Solved these Questions
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 5: ESTIMATING
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 6: FRACTIONS, DECIMALS, AND PERCENTS
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 3: PLUGGING IN THE ANSWER CHOICES
11 Videos
- PRACTICE TEST 4BOOK - PRINCETONCHAPTER - PRACTICE TEST 4EXERCISE - Math Test-Calculator
38 Videos
- SAT MATH: THE BIG PICTUREBOOK - PRINCETONCHAPTER - SAT MATH: THE BIG PICTUREEXERCISE - Example
4 Videos
Similar Questions
Knowledge Check
Two sides of a triangle measure 4 and 12. Which of the following could equal the length of the third side?
A5B7C9D20
The perimeter of an isosceles triangle is 49 m and the length of one of its equal sides is 17m. Find the length of the base of the triangle.
View SolutionThe area of an isosceles triangle having base 2 cm and the length of one of the equal sides 4 cm is
View SolutionJessica draws an isosceles triangle. The length of each of the two equal sides is twice as much as the length of the base. If the length of the base is x, find the rule for finding the perimeter of the triangle.
View SolutionThe area of an isosceles triangle is 60cm2 and the length of each one of its equal sides is 13 cm. Find its base.
View SolutionFind the area of an isosceles triangle having the base 6 cm and the length of each equal side 5 cm.
View SolutionThe area of an equilateral triangle ABC is 17320.5 cm2. With each vertex of the triangle as centre, a circle is drawn with radius equal to half the length of the side of the triangle (see Fig. 12.28). Find the area of the shaded region. (Use π=3.14and√3= 1.73205)
View SolutionThe perimeter of an isosceles triangle is 42cm and its base is (32) times each of the equal sides. Find the length of each side of the triangle, area of the triangle and the height of the triangle.
View Solution