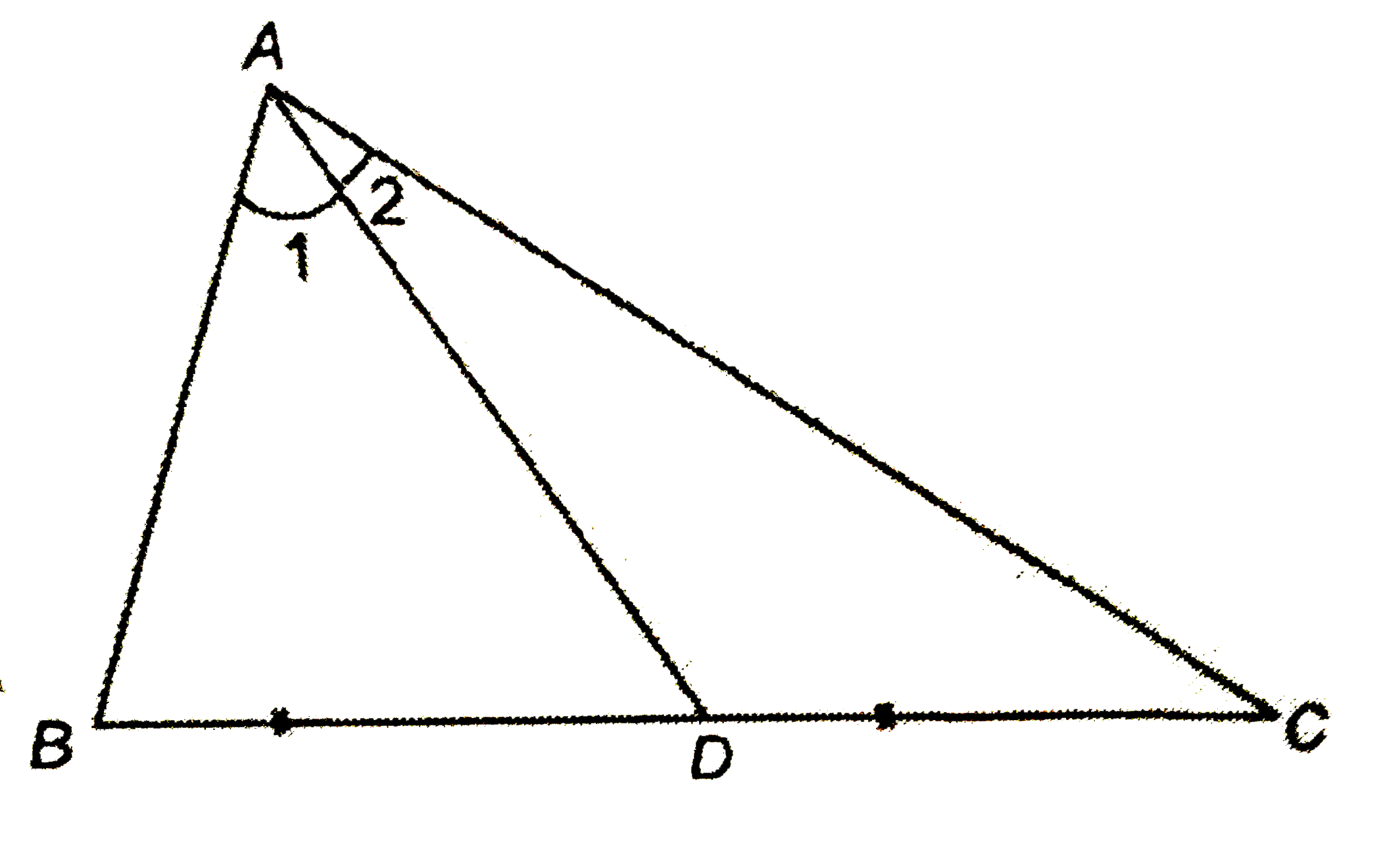
If the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : triangle A B C in which A D is the bisector of angle A meeting B C in D such that BD=DCTOPROVE: triangleA B C is an isosceles triangle.
It seems that for proving the triangles to be congruent, we have ∠1=∠2,AD=AD and BD=DC and so, triangles are congruent. But you see the ease of congruency. It is ASS , which is not the case of any congruency. So we will see this problem with a different view.
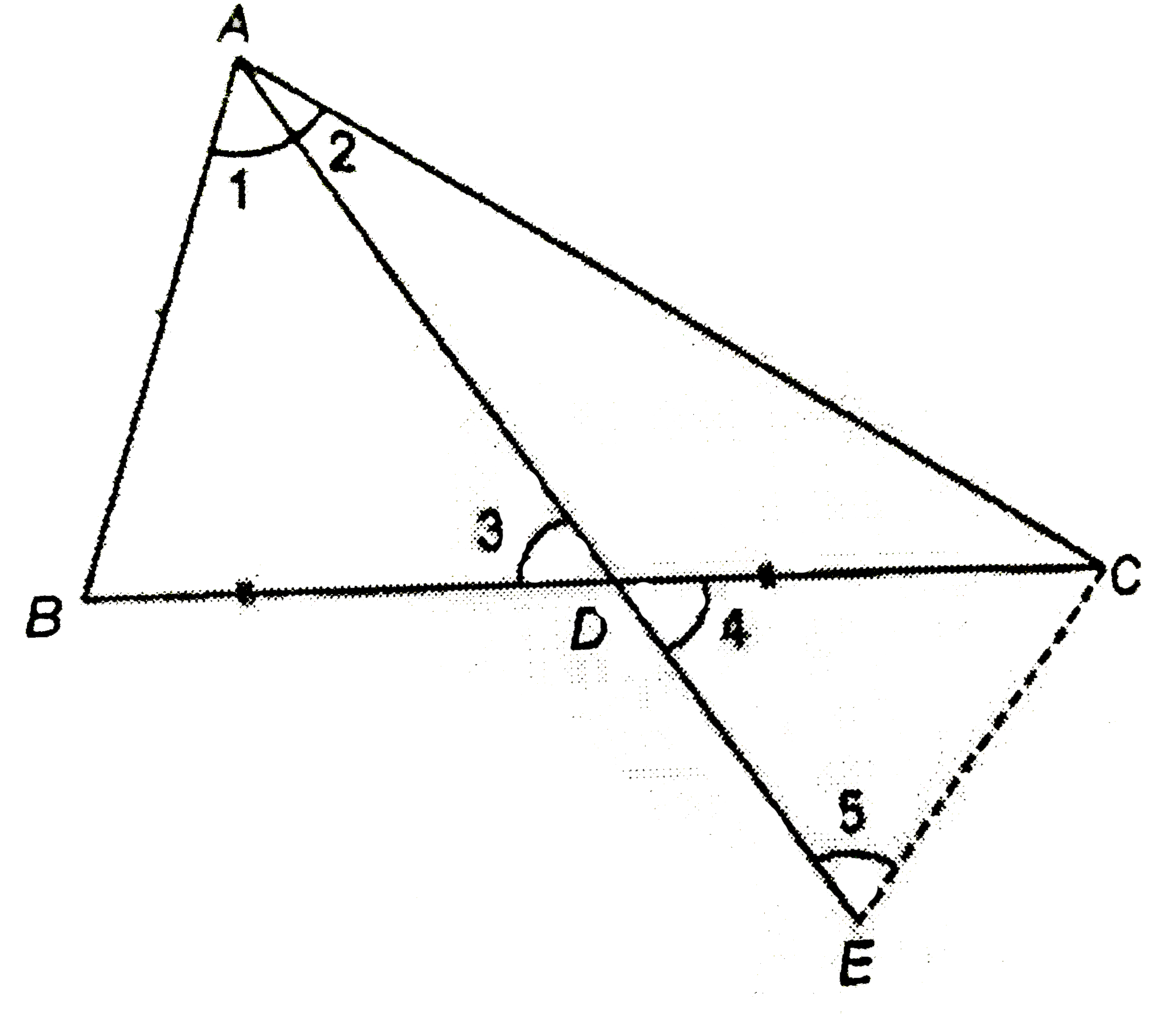
Construction : Produce AD to E such that AD=DE.
Proof : In ΔABD and ΔECD,
∵⎧⎪⎨⎪⎩BD=DC(Given as D is the mid-point)∠3=∠4(VOA)AD=DE(construction)
∴ΔABD≅ΔECD (SAS)
∴AB=EC (c.p.c.t) ...(1)
and ∠1=∠5 (c.p.c.t) ...(2)
But ∠1=∠2 (given) ...(3)
∴∠2=∠5 [fro (2) and (3)]
⇒ EC=AC ...(4)
( ∵ sides opposite to equal angles are equal)
∴ from (1) and (4), we have
AB=AC
∴ΔABC is an Isosceles triangle. Hence Proved.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View SolutionShow that the bisector of vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is (a) an isosceles triangle (b) an obtuse triangle (c) an equilateral triangle (d) a right triangle
View SolutionA triangle whose two sides are equal is called (a) an acute triangle (b) a scalene triangle (c) an isosceles triangle (d) an equilateral triangle
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIf all the vertices of a triangle have integral coordinates, then the triangle may be (a) right-angle (b) equilateral (c) isosceles (d) none of these
View SolutionABC is a triangle in which ∠A=720 , the internal bisectors of angles B and C meet in O . Find the magnitude of ∠BOC.
View Solution
