If the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
To prove that a triangle is isosceles when the bisector of the vertical angle bisects the base, we can follow these steps:
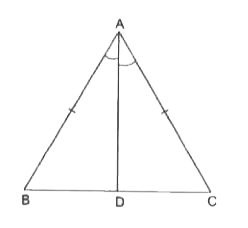
1. Given Information: Let triangle ABC be such that AD is the bisector of angle A, and D is the midpoint of the base BC. Therefore, BD = DC.
2. Construction: Extend AD to point E such that AD = DE. Join points C and E.
3. Triangles to Consider: We will consider triangles ABD and EDC.
4. Equal Sides:
- Since D is the midpoint of BC, we have BD = DC (given).
- From our construction, we have AD = DE (by construction).
5. Angles:
- Angle ADB = Angle CDE (by vertically opposite angles).
6. Congruence of Triangles:
- Now we have two sides and the included angle equal in triangles ABD and EDC:
- AB = AC (to be proved)
- BD = DC (given)
- AD = DE (by construction)
- Angle ADB = Angle CDE (vertically opposite angles)
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangle ABD is congruent to triangle EDC.
7. Corresponding Parts of Congruent Triangles:
- By the Corresponding Parts of Congruent Triangles (CPCT), we have:
- AB = EC
- AC = ED
8. Equal Angles:
- Since AD is the bisector of angle A, we have:
- Angle BAD = Angle CAD.
9. Conclusion:
- Since AB = AC, triangle ABC is isosceles.
- Since D is the midpoint of BC, we have BD = DC (given).
- From our construction, we have AD = DE (by construction).
- Angle ADB = Angle CDE (by vertically opposite angles).
- Now we have two sides and the included angle equal in triangles ABD and EDC:
- AB = AC (to be proved)
- BD = DC (given)
- AD = DE (by construction)
- Angle ADB = Angle CDE (vertically opposite angles)
- Therefore, by the Side-Angle-Side (SAS) congruence criterion, triangle ABD is congruent to triangle EDC.
- By the Corresponding Parts of Congruent Triangles (CPCT), we have:
- AB = EC
- AC = ED
- Since AD is the bisector of angle A, we have:
- Angle BAD = Angle CAD.
- Since AB = AC, triangle ABC is isosceles.
Topper's Solved these Questions
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Subjective Problems) ( Long Answer Type)5videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Subjective Problems) ( Integer/Numerical Value Type)5videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - TRIANGLESEXERCISE - EXERCISE (Subjective Problems) (Very Short Answer Type)9videos
TRIANGLES
- BOOK - MTG IIT JEE FOUNDATIONCHAPTER - STATISTICSEXERCISE - Olympiad/HOTS Corner20videos
STATISTICS
Similar Questions
Which of the following statements are true (T) and which are false (F): Side opposite to equal angles of a triangle may be unequal. Angle opposite to equal sides of a triangle are equal. The measure of each angle of an equilateral triangle is 600. If the altitude from one vertex of a triangle bisects the opposite side, then the triangle may be isosceles. The bisectors of two equal angles of a triangle are equal. If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles. The two altitudes corresponding to two equal sides of a triangle need not be equal. If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent. Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal to the hypotenuse and a side of the other triangle.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A ABC in which AD is the bisector of ∠A meeting BC in D such that BD=DC.
View SolutionIf the bisector of the vertical angle of a triangle bisects the base of the triangle;then the triangle is isosceles.
View SolutionJoinA→D
Hence,AD∥BC
∠ACB=∠CAD(alternateangle
∠BAC=∠ACD(alternateangle)
HenceAB=AC (by ASA congurency )so, it is isosceles triangle.View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
View SolutionProve that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
 View Solution
View SolutionShow that the bisector of vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionIf the bisectors of the base angles of a triangle enclose an angle of 1350, prove that the triangle is a right triangle.
View SolutionIf the bisectors of the base angles of a triangle enclose an angle of 1350, prove that the triangle is a right triangle.
View Solution
