If the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
135
78
57
101
The correct Answer is:A
To solve the problem, we need to evaluate the objective function Z=6x+3y at the given corner points of the feasible region, which are (15, 20), (40, 15), and (2, 72). We will then find the maximum and minimum values of Z and compute Zmax−Zmin.
1. Evaluate Z at the point (15, 20):
Z=6(15)+3(20)
Z=90+60=150
2. Evaluate Z at the point (40, 15):
Z=6(40)+3(15)
Z=240+45=285
3. Evaluate Z at the point (2, 72):
Z=6(2)+3(72)
Z=12+216=228
4. Determine Zmax and Zmin:
- From the calculations:
- Z(15,20)=150
- Z(40,15)=285
- Z(2,72)=228
- Therefore, Zmax=285 and Zmin=150.
5. Calculate Zmax−Zmin:
Zmax−Zmin=285−150=135
Thus, the final answer is:
Zmax−Zmin=135
Z=6(15)+3(20)
Z=90+60=150
Z=6(40)+3(15)
Z=240+45=285
Z=6(2)+3(72)
Z=12+216=228
- From the calculations:
- Z(15,20)=150
- Z(40,15)=285
- Z(2,72)=228
- Therefore, Zmax=285 and Zmin=150.
Zmax−Zmin=285−150=135
Zmax−Zmin=135
Topper's Solved these Questions
Similar Questions
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
View Solution
Knowledge Check
The corner points of a feasible region of a LPP are (0, 0), (0, 1) and (1, 0). If the objective function is Z = 7x + y, then Zmax−Zmin =
A0B1C7D6the corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
A(2,0),(2019,4519),(0,3)B(0,3),(2019,4519),(0,5)C(2,0),(2019,4519),(5,0)D(0,0),(2,0),(2019,4519),(0,3)The corner points of the feasible region of an LPP are (0,0),(0,8),(2,7),(5,4) and (6,0). The maximum value of the objective function Z = 3x + 2y is:
A20B23C27D18
The corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
View SolutionThe corner points of the feasible region of a system of linear inequalities are (0, 0), (4,0), (3,9), (1, 5) and (0, 3). If the maximum value of objective function, Z = ax + by occurs at points (3, 9) and (1, 5), then the relation between a and b is:
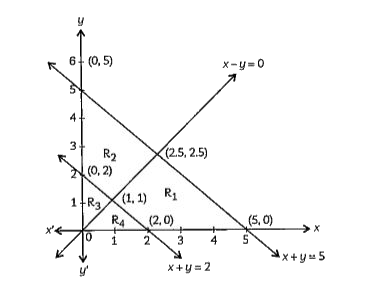
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
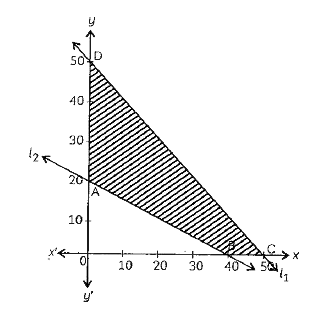
View SolutionThe feasible region of a system of linear inequalities is shown below. If the objective function is maximise Z = 25x + 15y, then the maximum value of Z occurs at:
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40). (20, 40), (60, 20). (60, 0). "The objective function is Z=4x+3y.
Compare the quantity in Column A and Column B.
Column AColumn BMaximum of Z325
View Solution
