The corner points of the feasible region determined by the system of linear constraints are (0, 0), (0, 40). (20, 40), (60, 20). (60, 0). "The objective function is Z=4x+3y.
Compare the quantity in Column A and Column B.
Column AColumn BMaximum of Z325
The quantity in column A is greater.
The quantity in column B is greater.
The two quantities are equal.
The relationship can not be determined on the basis of the information supplied.
To solve the problem, we need to evaluate the objective function Z=4x+3y at the given corner points of the feasible region and find the maximum value of Z. The corner points provided are (0, 0), (0, 40), (20, 40), (60, 20), and (60, 0).
1. Evaluate Z at (0, 0):
Z(0,0)=4(0)+3(0)=0
2. Evaluate Z at (0, 40):
Z(0,40)=4(0)+3(40)=120
3. Evaluate Z at (20, 40):
Z(20,40)=4(20)+3(40)=80+120=200
4. Evaluate Z at (60, 20):
Z(60,20)=4(60)+3(20)=240+60=300
5. Evaluate Z at (60, 0):
Z(60,0)=4(60)+3(0)=240+0=240
6. Determine the maximum value of Z:
The values of Z at the corner points are:
- At (0, 0): Z=0
- At (0, 40): Z=120
- At (20, 40): Z=200
- At (60, 20): Z=300
- At (60, 0): Z=240
The maximum value of Z is 300 at the point (60, 20).
Comparison:
- Column A: Maximum of Z=300
- Column B: Given value = 325
Now we compare the two quantities:
- Since 300<325, we conclude that the quantity in Column B is greater.
Final Answer:
The quantity in Column B is greater.
Z(0,0)=4(0)+3(0)=0
Z(0,40)=4(0)+3(40)=120
Z(20,40)=4(20)+3(40)=80+120=200
Z(60,20)=4(60)+3(20)=240+60=300
Z(60,0)=4(60)+3(0)=240+0=240
The values of Z at the corner points are:
- At (0, 0): Z=0
- At (0, 40): Z=120
- At (20, 40): Z=200
- At (60, 20): Z=300
- At (60, 0): Z=240
- Column A: Maximum of Z=300
- Column B: Given value = 325
- Since 300<325, we conclude that the quantity in Column B is greater.
The quantity in Column B is greater.
Topper's Solved these Questions
Similar Questions
The corner points of a feasible region determined by a system of linear inequations are (0,0),(4,0),(5,2),(2,2) and (0, 1). If the objective function is Z = x + y, then maximum of Z occurs at:
View SolutionThe corneer points of a feasible region, determined by a system of linear inequations, are (0,0),(1,0),(4,3),(2,1)and(0,1). If the objective function is Z=2x−3y, then the minimum value of Z is :
View Solution
Knowledge Check
The corner points of the feasible region determined by the system of linear contraints are (0,0), (0,40),( 20,40),(60,20),(60,0). The objective function is Z=4x+3y. Compare the quantity in Column A and Column B.
 AThe quantity in Column A is greaterBThe quantity in column B is greaterCThe two quantities are equal.DThe relationship cannot be determined on the basis of the information supplied.
AThe quantity in Column A is greaterBThe quantity in column B is greaterCThe two quantities are equal.DThe relationship cannot be determined on the basis of the information supplied.The corner points of the feasible region determined by a system of linear inequations are (0,0),(4,0),(2,4) and (0,5). If the minimum value of Z=ax+by,a, b>0 occurs at (2,4) and (0,5) ,then :
Aa=2bB2a=bCa=bD3a=bIf the corner points of a feasible region of system of linear inequalities are (15,20) (40,15) and (2,72) and the objective function is Z = 6x + 3y then Zmax−Zmin =
A135B78C57D101
The corner points of a feasible region determined by a system of linear inequalities are (20,40),(50,100),(0,200) and (0,50). If the objective funtion Z=x+2y, then maximum of Z occurs at.
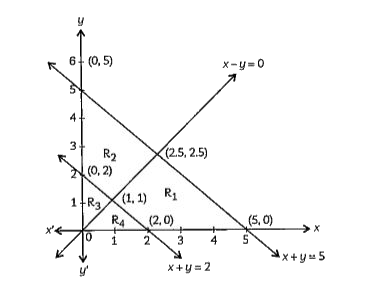
View SolutionThe corner points of the feasible region of the system of linear inequations x+y≥2,x+y≤5,x−y≥0,x,y≥0 are :
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0, 10), (5, 5) (15, 15), (0, 20). Let Z = px + qy , where p,q>0. Then, the condition on p and q so that the maximum of Z occurs at both the points (15, 15) and (0, 20), is
View Solutionthe corner points of the feasible region of a system of linear inequalities 3x+5y≤15,5x+2y≥10,x≥0,y≥0, are:
View SolutionThe corner points of the feasible region determined by the system of linear constraints are (0,10) , (5,5) (25,20),(0,30) Let z = px + qy , where p,q>0 Condition on p and q so that te maximum of z occurs at both the points (25,20 ) and (0,30) is ………
View Solution
