If the height and radius of a cone of volume V are doubled, then the volume of the cone, is (a) 3 V (b) 4 V (c) 6 V (d) 8 V
To solve the problem, we need to determine how the volume of a cone changes when both its height and radius are doubled.
1. Understand the Volume Formula:
The volume V of a cone is given by the formula:
V=13πr2h
where r is the radius and h is the height of the cone.
2. Define Initial Dimensions:
Let the initial height of the cone be h=x and the radius be r=y. Therefore, the initial volume V can be expressed as:
V=13πy2x
3. Double the Dimensions:
If we double the height and radius, the new height becomes h′=2x and the new radius becomes r′=2y.
4. Calculate the New Volume:
Substitute the new dimensions into the volume formula:
V′=13π(r′)2(h′)=13π(2y)2(2x)
Simplifying this:
V′=13π(4y2)(2x)=13π⋅8y2x
5. Relate New Volume to Initial Volume:
Notice that:
V′=8(13πy2x)=8V
Thus, the new volume V′ is 8 times the original volume V.
6. Conclusion:
Therefore, if the height and radius of the cone are doubled, the volume of the cone becomes:
V′=8V
Final Answer:
The volume of the cone when both the height and radius are doubled is (d) 8V.
The volume V of a cone is given by the formula:
V=13πr2h
where r is the radius and h is the height of the cone.
Let the initial height of the cone be h=x and the radius be r=y. Therefore, the initial volume V can be expressed as:
V=13πy2x
If we double the height and radius, the new height becomes h′=2x and the new radius becomes r′=2y.
Substitute the new dimensions into the volume formula:
V′=13π(r′)2(h′)=13π(2y)2(2x)
Simplifying this:
V′=13π(4y2)(2x)=13π⋅8y2x
Notice that:
V′=8(13πy2x)=8V
Thus, the new volume V′ is 8 times the original volume V.
Therefore, if the height and radius of the cone are doubled, the volume of the cone becomes:
V′=8V
The volume of the cone when both the height and radius are doubled is (d) 8V.
Topper's Solved these Questions
- SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDERBOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A RIGHT CIRCULAR CYLINDEREXERCISE - All Questions
133 Videos
- SURFACE AREA AND VOLUME OF A SPHERE BOOK - RD SHARMA ENGLISHCHAPTER - SURFACE AREA AND VOLUME OF A SPHERE EXERCISE - All Questions
140 Videos
Similar Questions
If each edge of a cube, of volume V, is doubled, then the volume of the new cube is (a) 2 V (b) 4 V (c) 6 V (d) 8 V
View SolutionA right circular cylinder and a right circular cone have the same radius and the same volume. The ratio of the height of the cylinder to that of the cone is (a) 3:5 (b) 2:5 (c) 3:1 (d) 1:3
View SolutionA cylinder with base radius of 8 cm and height of 2 cm is melted to form a cone of height 6 cm. The radius of the cone is
(a) 4 cm
(b) 5 cm
(c) 6 cm
(d) 8 cm
View SolutionA solid consists of a circular cylinder with an exact fitting right circular cone placed at the top. The height of the cone is h . If the total volume of the solid is 3 times the volume of the cone, then the height of the circular cylinder is (a) 2h (b) 2h3 (c) 3h2 (d) 4h
View SolutionIf the radius of a right circular cone is halved and height is doubled then what will be new volume?
View SolutionThe curved surface are of a cone of height 8 m is 188.4 m2 .Find the volume of cone
View SolutionIf l is the length of a diagonal of a cube of volume V, then (a) 3V=l3 (b) √3 V=l3 (c) 3√3 V=2l3 (d) 3√3 V=l3
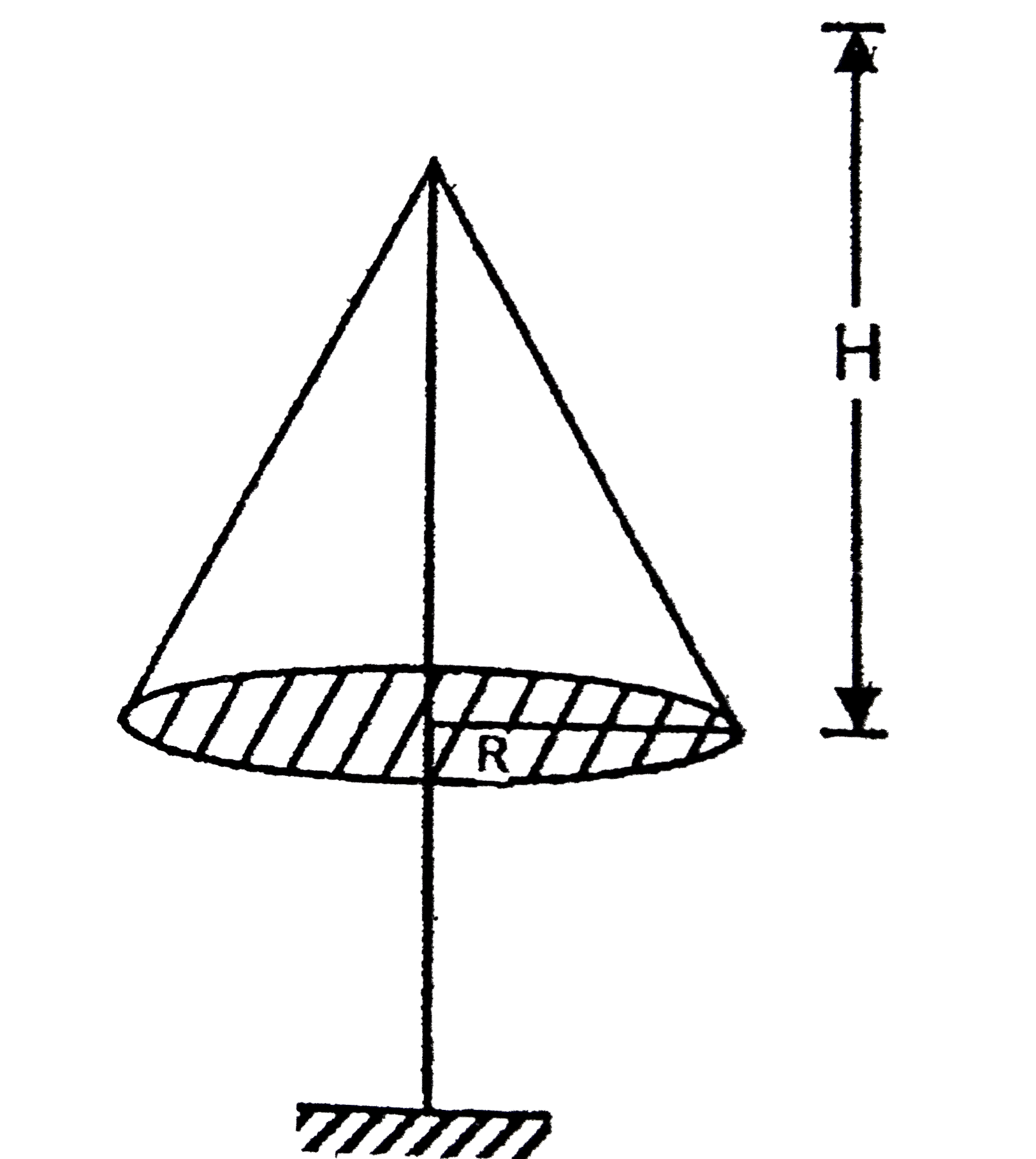
View SolutionA solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is R and the volume of the cone is V. In equilibrium the base of the cone is at a depth H below the water surface. Density of wood is d(<ρ, density of water) Then tension in the string is
View SolutionThe ratio of the heights of two cones of same base is 4 : 3. If the volume of small cone is 462πcm3, then find the volume of new cone.
View SolutionA given right cone has volume p, and the largest right circular cylinder that can be inscribed in the cone has volume q. Then p:q is (a) 9:4 (b) 8:3 (c) 7:2 (d) none of these
View Solution
