A solid wooden cone has been supported by a string inside water as shown in the figure. The radius of the circular base of the cone is $R$ and the volume of the cone is $V$ . In equilibrium the base of the cone is at a depth $H$ below the water surface. Density of wood is $d (< ρ$ , density of water) Then tension in the string is

A

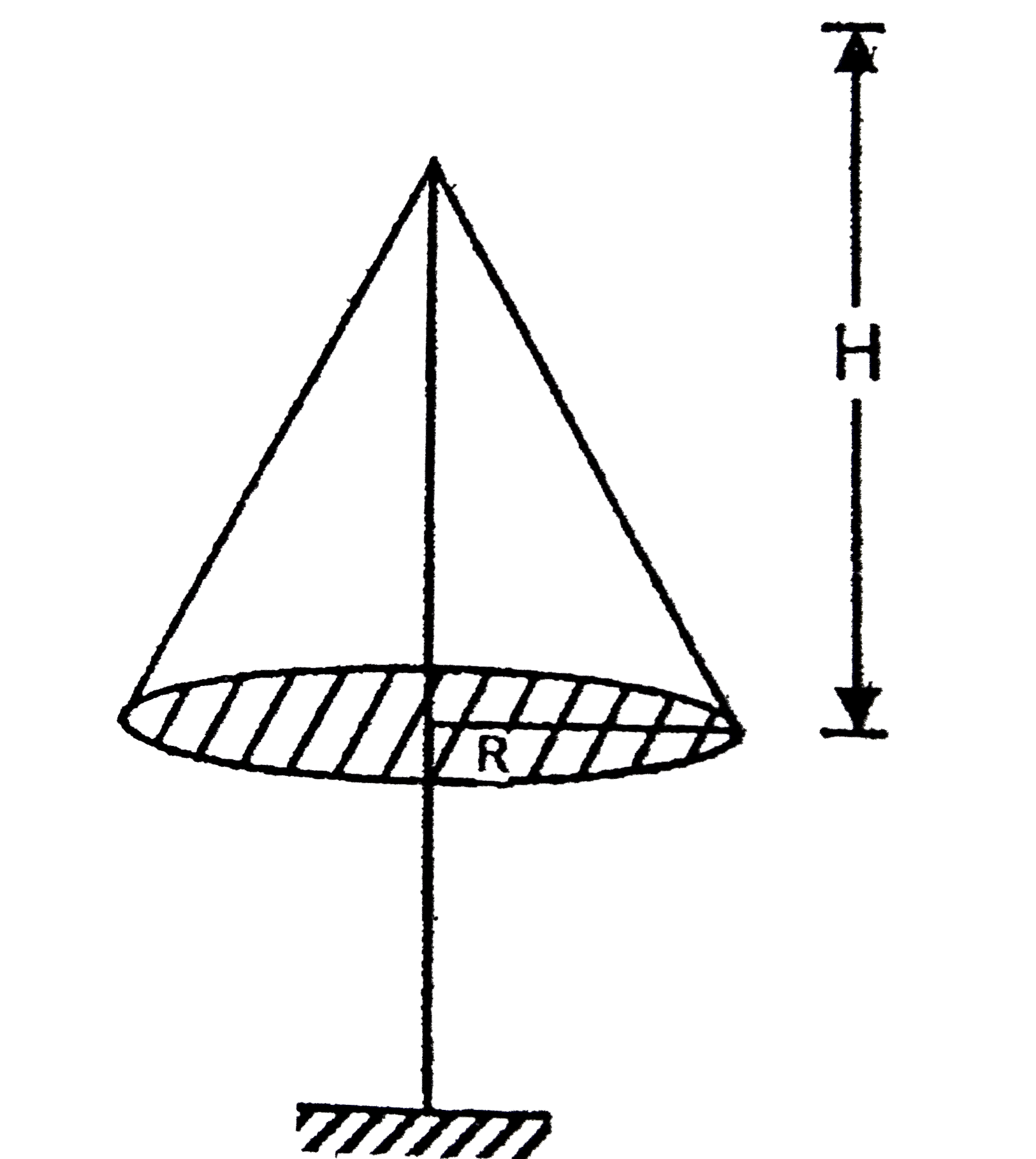
$V g (ρ - d)$

B

$V g (d + ρ)$

C

$2 V g (ρ - d)$

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

(a) Buoyancy force is $F_{B} = v ρ g$
Weight of the cone $W = v d g$
$∴$ Tension $T = W - F_{a} = v g (d - ρ)$
(b) $F_{B} - v ρ g$
Buoyancy is resultant of vertically upward force $(F_{1})$ applied by water perssure on the base of the cone
and the vertically downward force $(F_{2})$ applied by water on the slant surface. [The horizontal component of this force same up to zero due to symmetry

$∴ F_{1} - F_{2} = F_{B}$
$π R^{2} . [ρ_{0} + ρ g H] - F_{2} = v ρ g$
$∴ F_{2} = π R^{2} [ρ_{0} + ρ g H] - v ρ g$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

RESONANCE ENGLISH-TEST PAPERS-PHYSICS

Home
Ask Doubt
Profile