If the length of a chord AB is equal to the radius OA of the circle, then ∠ABO equals (O is the center)

120∘
60∘
45∘
30∘
The correct Answer is:B
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - TEST YOURSELF (MULTIPLE CHOICE QUESTION)
24 Videos
- ALGEBRAIC EXPRESSIONS AND POLYNOMIALS BOOK - CENGAGECHAPTER - ALGEBRAIC EXPRESSIONS AND POLYNOMIALS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
- LAWS OF EXPONENTS AND LOGARITHMS BOOK - CENGAGECHAPTER - LAWS OF EXPONENTS AND LOGARITHMS EXERCISE - OLYMPIAD AND NTSE LEVEL EXERCISES
10 Videos
Similar Questions
In the figure , in a circle with centre O, length of chord AB is equal to the radius of the circle. Find the measure of each of the following :
(1) ∠AOB
(2) ∠ACB
(3) arc AB
(4) arc ACB
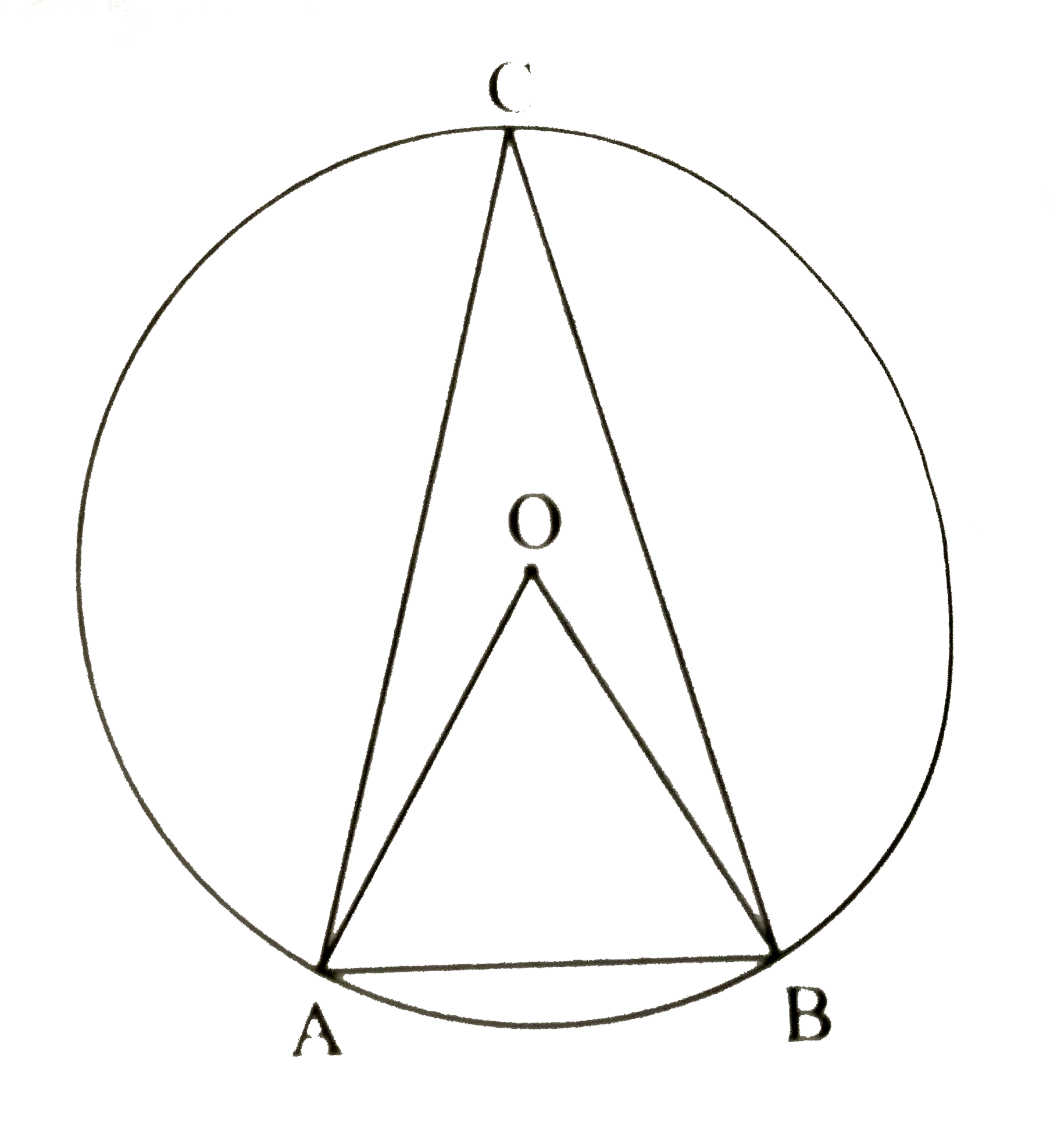
View SolutionIn the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View Solution
Knowledge Check
If the length of a chord of a circle is equal to that of the radius of the circle , then the angle subtended , in radians , at the centre of the circle by the chord is
A1Bπ2Cπ3Dπ4The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to :
A30∘B45∘C60∘D90∘The length of a chord of a circle is equal to the radius of the circle. The angle which this chord subtends in the major segment of the circle is equal to
A30∘B45∘C60∘D90∘
In the adjoining figure, O is the centre of the circle. If the chord AB is equal to the radius of the circle, then find the value of ∠ADB.

View SolutionIn the figure, in a circle with centre O, length of chord AB is equal to the radius of the circle. Find measure of each of the following.
∠AOB
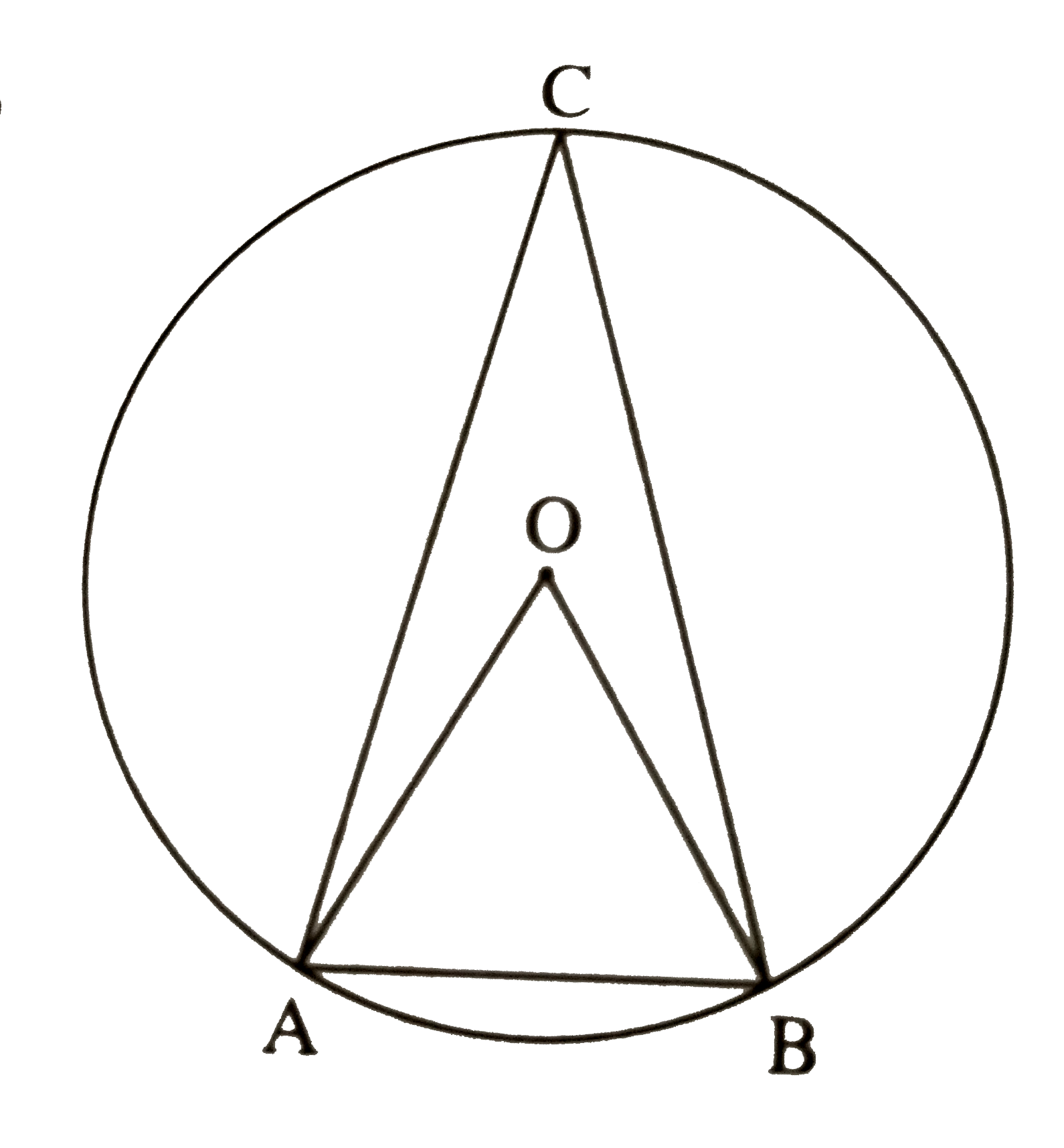
View SolutionThe length of a chord of a circle is equal to the radius of the circle. Compare the distance of the chord from the centre with the radius of the circle.
View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View Solution
