If the line y=3x−15 intersects the line y=mx+8 in the third quadrant, which of the follwing must be true ?
m is positive
m is negative
m = 0
0<m<1
The correct Answer is:A
To solve the problem, we need to determine the conditions under which the lines y=3x−15 and y=mx+8 intersect in the third quadrant.
1. Set the equations equal to each other:
Since both equations represent y, we can set them equal to find the intersection point:
3x−15=mx+8
2. Rearrange the equation:
Move all terms involving x to one side and constant terms to the other side:
3x−mx=15+8
This simplifies to:
(3−m)x=23
3. Solve for x:
Now, we can express x in terms of m:
x=233−m
4. Determine the sign of x:
For the intersection to occur in the third quadrant, both x and y must be negative. Since y=mx+8 must also be negative, we first analyze x:
- For x to be negative, the denominator (3−m) must be positive (because 23 is positive). Therefore:
3−m>0⟹m<3
5. Determine the sign of y:
Next, we substitute x back into one of the equations to find y:
Using y=3x−15:
y=3(233−m)−15
Simplifying this gives:
y=693−m−15
To ensure y<0:
69−15(3−m)3−m<0
Simplifying the numerator:
69−45+15m<0⟹15m<−24⟹m<−2415⟹m<−1.6
6. Combine the inequalities:
We have two inequalities:
- m<3
- m<−1.6
Since m must be less than both values, the more restrictive condition is:
m<−1.6
Conclusion:
The line y=mx+8 intersects the line y=3x−15 in the third quadrant if m<−1.6.
Since both equations represent y, we can set them equal to find the intersection point:
3x−15=mx+8
Move all terms involving x to one side and constant terms to the other side:
3x−mx=15+8
This simplifies to:
(3−m)x=23
Now, we can express x in terms of m:
x=233−m
For the intersection to occur in the third quadrant, both x and y must be negative. Since y=mx+8 must also be negative, we first analyze x:
- For x to be negative, the denominator (3−m) must be positive (because 23 is positive). Therefore:
3−m>0⟹m<3
Next, we substitute x back into one of the equations to find y:
Using y=3x−15:
y=3(233−m)−15
Simplifying this gives:
y=693−m−15
To ensure y<0:
69−15(3−m)3−m<0
Simplifying the numerator:
69−45+15m<0⟹15m<−24⟹m<−2415⟹m<−1.6
We have two inequalities:
- m<3
- m<−1.6
m<−1.6
The line y=mx+8 intersects the line y=3x−15 in the third quadrant if m<−1.6.
Topper's Solved these Questions
- COORDINATE GEOMETRY BOOK - KAPLANCHAPTER - COORDINATE GEOMETRY EXERCISE - COORDINATE GEOMETRY FOLLOW - UP TEST
6 Videos
- CIRCLESBOOK - KAPLANCHAPTER - CIRCLESEXERCISE - Multiple Choice Question
12 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS BOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONS EXERCISE - Multiple Choice Question
20 Videos
Similar Questions
Knowledge Check
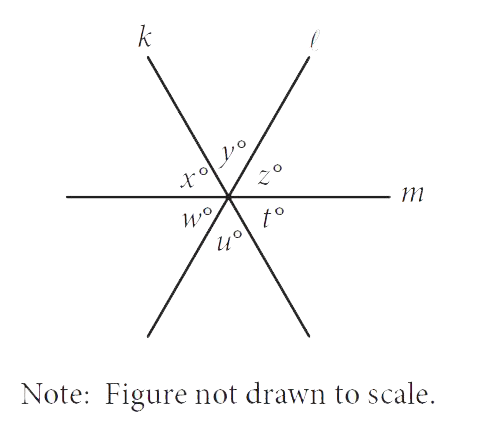
In the figure above, lines k, A , and m intersect at a point. If x+y=u+w , which of the following must be true?
I. x=z
II. Y=w
iii. Z=tAI and II onlyBI and III onlyCII and III onlyDI, II, and IIIIn the figure, the equation of the line is y=910x+k. Which one of the following must be true about line segement AO and BO?
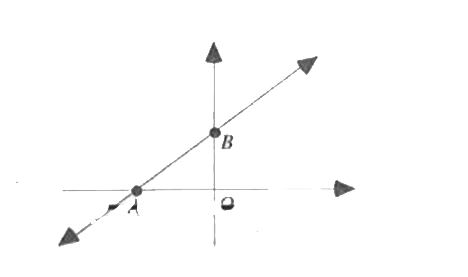 AAO gt BOBAO lt BOCAO≤BODAO=BO
AAO gt BOBAO lt BOCAO≤BODAO=BO
The line through (4,3)and(−6,0) intersects the line 5x+y=0. Find the angles of intersection.
View SolutionIf the line y=mx meets the lines x+2y−1=0 and 2x−y+3=0 at the same point, then m is equal to
View SolutionThe lines x+y=|a|andax−y=1 intersect each other in the first quadrant. Then the set of all possible values of a is the interval:
View SolutionIf the line y=mx, meets the lines x+2y=1 and 2x−y+3=0 at one point only then m=?
View SolutionThe point (2,1) , translated parallel to the line x−y=3 by the distance of 4 units. If this new position A' is in the third quadrant, then the coordinates of A' are-
View SolutionA circle touches both the x-axis and the line 4x−3y+4=0. Its centre is in the third quadrant and lies on the line x−y−1=0. Find the equation of the circle.
View Solution
