If the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respectively, then find the equation of the side AB.
The correct Answer is:x-y+12=0
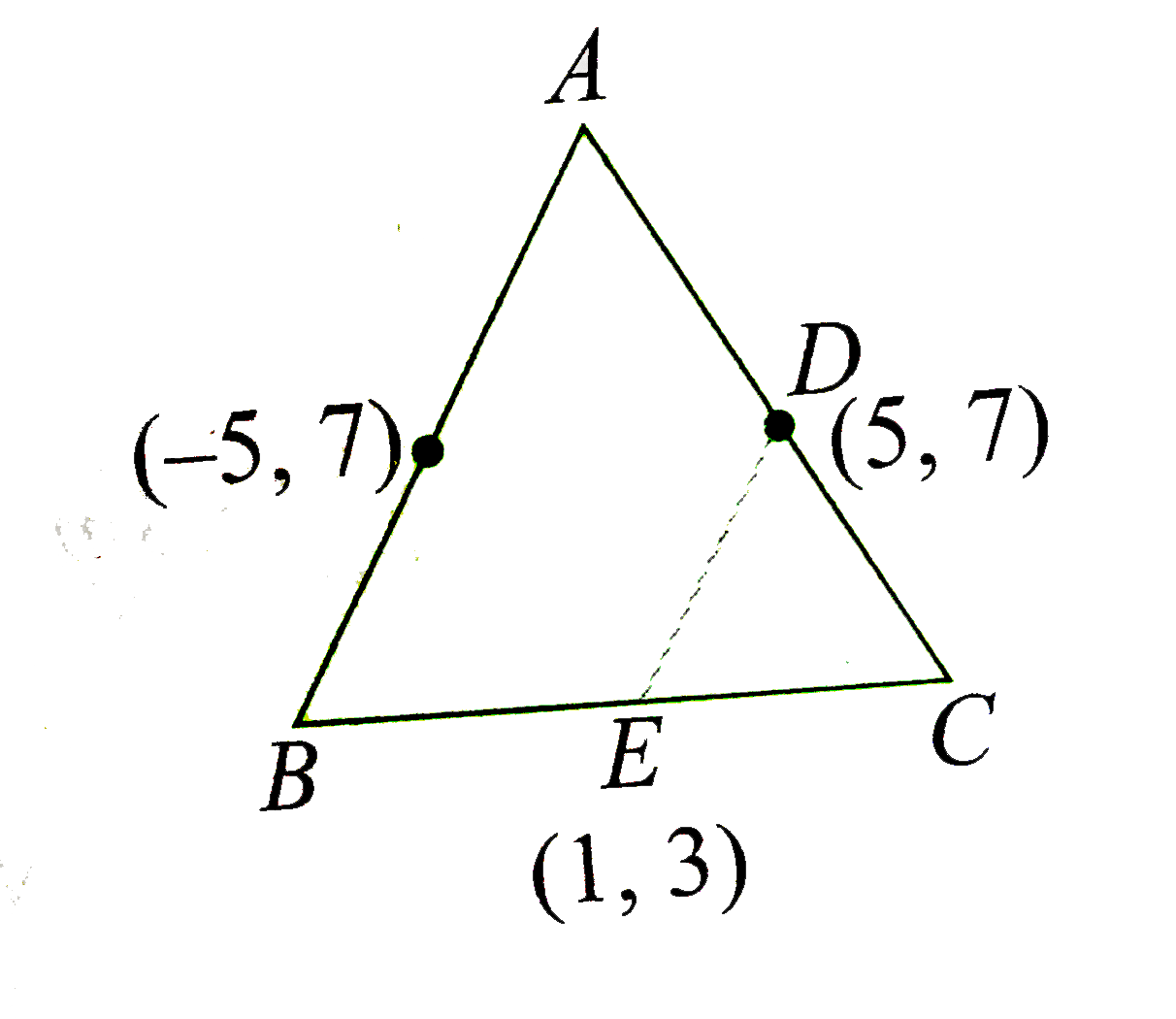
Slope of DE =7−35−1=1
Slope of AB =1
Hence, the equation of AB is
y-7=x+5
or x-y+12=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.2
4 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.3
7 Videos
- STRAIGHT LINESBOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - JEE Advanced Previous Year
4 Videos
- STRAIGHT LINEBOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type
8 Videos
- THEORY OF EQUATIONSBOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year
9 Videos
Similar Questions
If the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respec-tively, then find the equation of the side AB.
View SolutionIf the middle points of the sides BC,CA, and AB of triangle ABC are (1,3),(5,7), and (−5,7), respectively, then find the equation of the side AB.
View Solution
Knowledge Check
The vertices of a triangle are (A(−1,−7),B(5,1), and C(1,4). The equation of the bisector of ∠ABC is____
Ax + 7y - 2 = 0Bx - 7y - 2 = 0Cx - 7y + 2 = 0DNone of these
The altitudes from the angular points A,B and C on the opposite sides BC,CA and AB of ΔABC 'are 210,195 and 182 respectively. If the length of the side BC can be expressed as rational mn (in the lowest form), then find (m+n).
View SolutionThe origin is the centroid of a triangle ABC is at the point G(1,1,1). If the coordinates of A and B are (3,-5,7) an (-1,7,-6) respectively, then find the coordinates of the point C.
View SolutionFind the lengths of the altitudes of the triangle whose vertices are A(1,3),B(5,-6) and C(7,-4) ,
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,-5,7) and (-1,7,-6) respectively, find the coordinates of the point C.
View SolutionFind the lengths of the medians AD and BE of ΔABC whose vertices are A(7, -3), B(5, 3) and C(3, -1).
View SolutionThe centroid of ∆ABC is at (1, 1, 1). If coordinates of A and B are (3,–5, 7) and (–1, 7, –6) respectively, find coordinates of point C.
View SolutionThe centroid of a triangle ABC is at the point (1,1,1). If the coordinates of A and B are (3,5,7)and (1,7,6), respectively, find the coordinates of the point C.
View Solution
