If the mode of the data: 64, 60, 48, x, 43, 48, 43, 34 is 43, then x+3= (a) 44 (b) 45 (c) 46 (d) 48
To solve the problem step by step, we need to find the value of x such that the mode of the given data set is 43. The data set is:
64,60,48,x,43,48,43,34
Step 1: Understand the concept of mode
The mode of a data set is the number that appears most frequently. In this case, we are given that the mode is 43.
Step 2: Count the occurrences of each number
Let's list the numbers and their occurrences, excluding x:
- 64: 1 time
- 60: 1 time
- 48: 2 times
- 43: 2 times
- 34: 1 time
Step 3: Analyze the current mode
Currently, the numbers 43 and 48 both appear 2 times. For 43 to remain the mode, it must appear more frequently than any other number.
Step 4: Determine the value of x
To ensure that 43 is the mode, x must be equal to 43. If x=43, the occurrences would be:
- 64: 1 time
- 60: 1 time
- 48: 2 times
- 43: 3 times (because we now have an additional 43 from x)
- 34: 1 time
Now, 43 appears 3 times, which is more than any other number.
Step 5: Calculate x+3
Since we found that x=43, we can now calculate:
x+3=43+3=46
Conclusion
Thus, the value of x+3 is:
46
Answer: (c) 46
---
The mode of a data set is the number that appears most frequently. In this case, we are given that the mode is 43.
Let's list the numbers and their occurrences, excluding x:
- 60: 1 time
- 48: 2 times
- 43: 2 times
- 34: 1 time
Currently, the numbers 43 and 48 both appear 2 times. For 43 to remain the mode, it must appear more frequently than any other number.
To ensure that 43 is the mode, x must be equal to 43. If x=43, the occurrences would be:
- 60: 1 time
- 48: 2 times
- 43: 3 times (because we now have an additional 43 from x)
- 34: 1 time
Since we found that x=43, we can now calculate:
Thus, the value of x+3 is:
Topper's Solved these Questions
Similar Questions
Find the mean deviation from the mean for the following data:
38, 70, 48, 40, 42, 55, 63, 46, 54, 44View SolutionIn Fig.72, if AB∣∣CD and AE∣∣BD, then the value of x
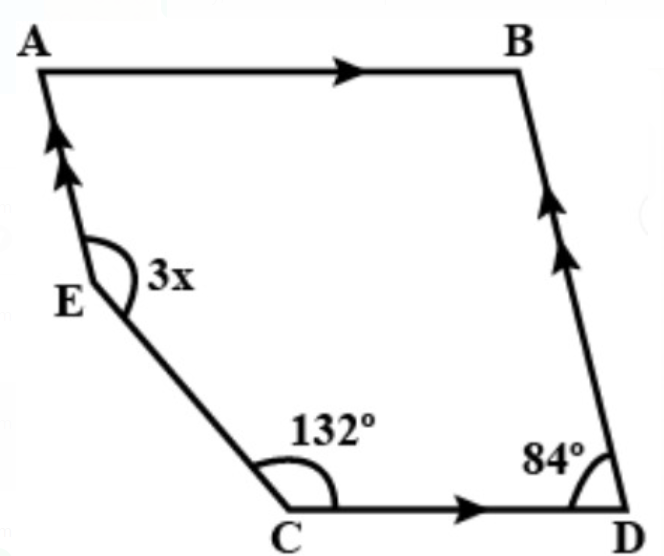 is
(a) 38 (b) 48
(b) 58 (d) 68View Solution
is
(a) 38 (b) 48
(b) 58 (d) 68View SolutionIf the mean of observations is then 43 (b) 42 44 (d) 45
View SolutionIn Figure, for which value of x is l1l2 ? 37 (b) 43 (c) 45 (d) 47
View Solution2+310+4100= ? (a) 2.304 (b) 0.403 (c) 2.34 (d) 2.43
View SolutionIn the given figure, the value of x is
(a) 720
(b) 500
(c) 580
(d) 480View SolutionThe ratio of two numbers is 3:4 and their HCF is 4. Their LCM is
(a) 12
(b) 16
(c) 24
(d) 48View SolutionThe weights (in kg.) of 15 students of a class are:38, 42, 35, 37, 45, 50, 32, 43, 43, 40, 36, 38, 43, 38, 47(i) Find the mode and median of this data.(ii) Is there more than one mode?
View SolutionThe value of 0.23+ 0.22 is (a) 0.45 (b) 0.43 (c) 0.47 (d) 0.41
View SolutionFind the median of the following observations: 46, 64, 87, 41, 58, 77, 35, 90, 55, 92, 33. If 92 is replaced by 99 and 41 by 43 in the above data, find the new median?
View Solution

