If the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of ΔABC, then identify the type of ΔABC
isosceles triangle
equilateral triangle
right angled triangle
None of these
The correct Answer is:D
Step by step video & image solution for If the perimeter of the triangle formed by feet of altitudes of the triangle ABC is equal to four times the circumradius of Delta ABC, then identify the type of Delta ABC by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (More Than One Correct Option Type Questions)
23 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Statement I And Ii Type Questions)
11 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - PROPERTIES AND SOLUTIONS OF TRIANGLES EXERSISE 1: SINGLE OPTION CORRECT TYPE QUESTIONS
1 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
51 Videos
- SEQUENCES AND SERIESBOOK - ARIHANT MATHS ENGLISHCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos
Similar Questions
Knowledge Check
In the figure, what is the area of ΔABC?
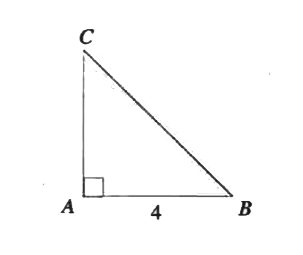 A6B7C8DIt cannot be determined from the information given
A6B7C8DIt cannot be determined from the information givenIn the figure, what is the area of ΔABC?
 A2B√2C1D1/2
A2B√2C1D1/2What is the perimenter of Triangle ABC in the figure?
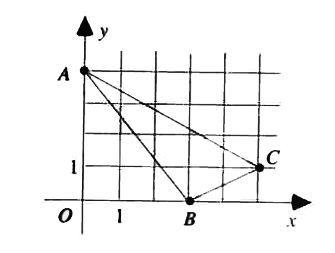 A5+√5+√34B10+√34C5+√5+√28D2√5+√34
A5+√5+√34B10+√34C5+√5+√28D2√5+√34
H is orthocenter of the triangle ABC, then AH is equal to :
View SolutionIf the radius of the circumcircle of the isosceles triangle ABC is equal to AB(=AC), then the angle A is equal to-
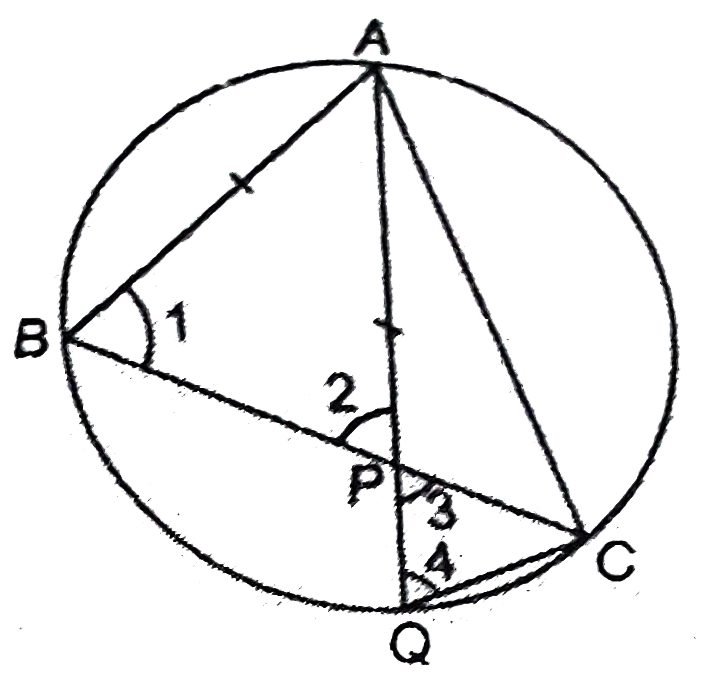
View SolutionIn given figure , ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
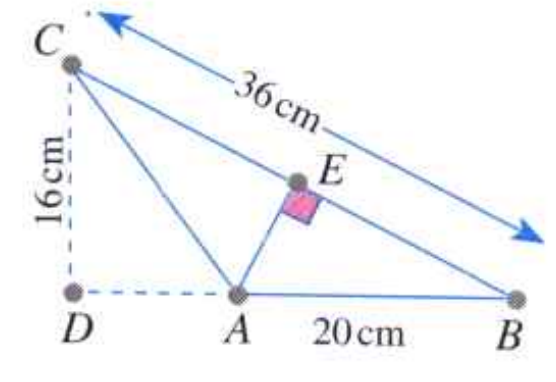
View SolutionIn the given triangle ABC, find AE.
View SolutionIn triangle ABC, R(b+c)=a√bc, where R is the circumradius of the triangle. Then the triangle is
View Solution
