In a triangle ABC
sinA. sinB.sinC =Δ2R2
sinA.sinB.sinC =r2R(sinA+sinB+sinC)
acosA+bcosB+ccosC=abc2R2
sinA.sinB.sinC=R2r(sinA+sinB+sinC)
The correct Answer is:A, B
To solve the problem regarding the triangle ABC and to verify the given equation, we will follow these steps:
1. Identify the Given Information:
We have a triangle ABC with sides a, b, and c opposite to angles A, B, and C respectively. We need to verify the equation:
sinA⋅sinB⋅sinC=Δ2R2
where Δ is the area of the triangle and R is the circumradius.
2. Area of Triangle:
The area Δ of triangle ABC can be expressed using the formula:
Δ=12absinC
3. Using the Sine Rule:
According to the sine rule:
asinA=bsinB=csinC=2R
From this, we can express the sides in terms of the angles and the circumradius R:
a=2RsinA,b=2RsinB,c=2RsinC
4. Substituting Values in Area Formula:
Now, substituting the values of a and b into the area formula:
Δ=12(2RsinA)(2RsinB)sinC
Simplifying this, we get:
Δ=2R2sinAsinBsinC
5. Expressing Δ in Terms of R:
Now, we can express Δ in terms of R:
Δ=2R2sinAsinBsinC
6. Finding Δ2R2:
To find Δ2R2:
Δ2R2=sinAsinBsinC
7. Conclusion:
Thus, we have shown that:
sinA⋅sinB⋅sinC=Δ2R2
Therefore, the equation is verified, and the first option is correct.
We have a triangle ABC with sides a, b, and c opposite to angles A, B, and C respectively. We need to verify the equation:
sinA⋅sinB⋅sinC=Δ2R2
where Δ is the area of the triangle and R is the circumradius.
The area Δ of triangle ABC can be expressed using the formula:
Δ=12absinC
According to the sine rule:
asinA=bsinB=csinC=2R
From this, we can express the sides in terms of the angles and the circumradius R:
a=2RsinA,b=2RsinB,c=2RsinC
Now, substituting the values of a and b into the area formula:
Δ=12(2RsinA)(2RsinB)sinC
Simplifying this, we get:
Δ=2R2sinAsinBsinC
Now, we can express Δ in terms of R:
Δ=2R2sinAsinBsinC
To find Δ2R2:
Δ2R2=sinAsinBsinC
Thus, we have shown that:
sinA⋅sinB⋅sinC=Δ2R2
Therefore, the equation is verified, and the first option is correct.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section D (Linked Comprehension Type Questions)27videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section E (Assertion-Reason Types Questions)18videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section-B (Objective Type Questions One option is correct)131videos
TRIGNOMETRIC FUNCTIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - J10videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - SECTION-J (Aakash Challengers Questions)5videos
VECTOR ALGEBRA
Similar Questions
Knowledge Check
- Question 1 - Select One
By which postulate or theorem are triangle ABC and triangle DBC congruent ?
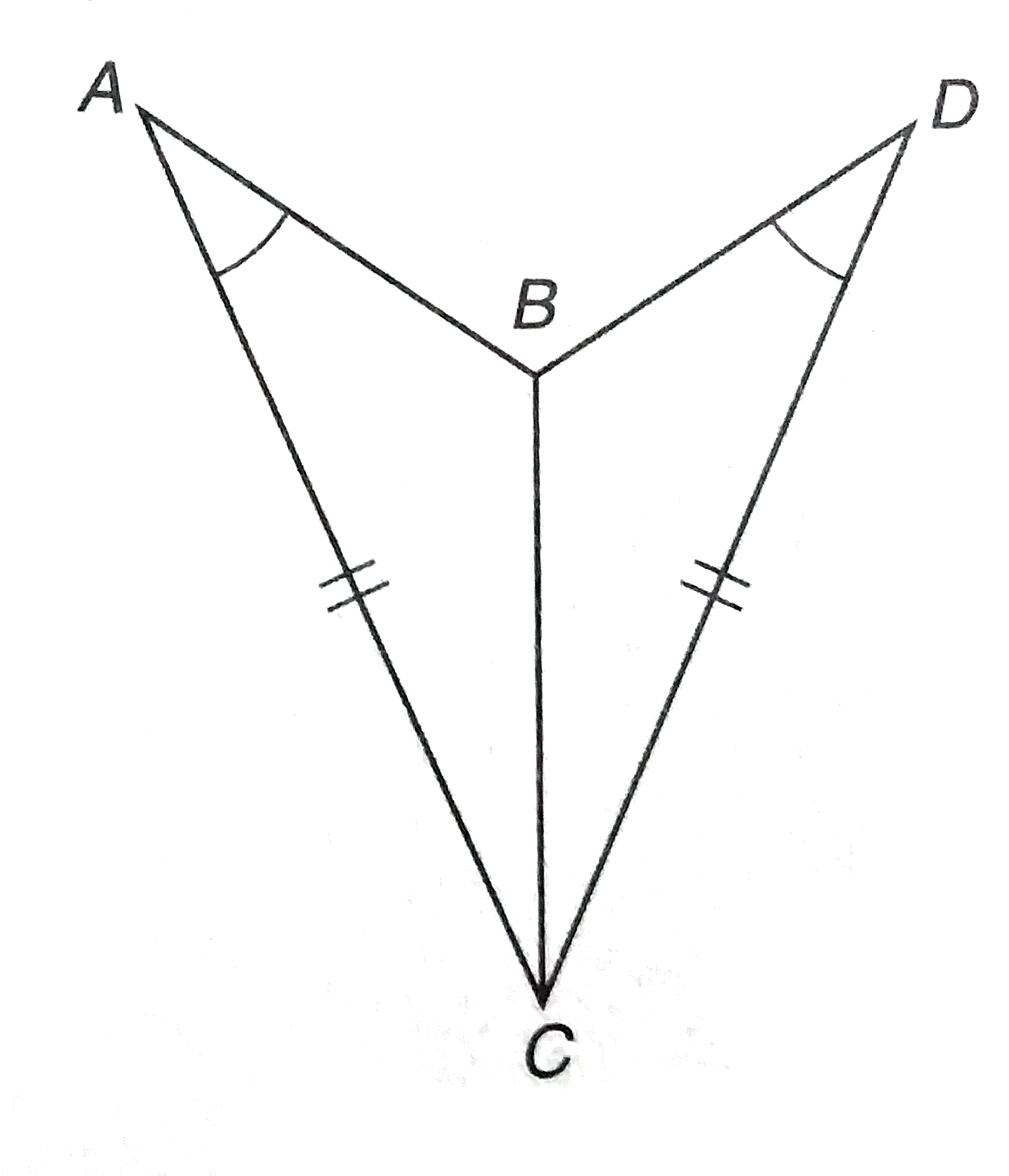 ASASBSSSCAASDCannot be determined from the given information.
ASASBSSSCAASDCannot be determined from the given information.
In any triangle ABC, if the angle bisector of ∠A and perpendicular bisector of BC intersect, prove that they intersect on the circumcircle of the triangle ABC.
View SolutionIn any triangle ABC, if the angle bisector of ∠Aand perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
View SolutionIf →a,→b,→c are the position vectors of the vertices. A,B,C of a triangle ABC. Then the area of triangle ABC is
View SolutionConstruct a triangle ABC in which BC = 8 cm, angle B = 45° and angle C = 30° Construct another triangle similar to Delta ABC such that its sides are 3/4. of the corresponding sides of Delta ABC.
View SolutionLet G be the centroid of triangle ABC and the circumcircle of triangle AGC touches the side AB at A
If AC = 1, then the length of the median of triangle ABC through the vertex A is equal toView SolutionThere can exist a triangle ABC satisfying the conditions :
View SolutionWhich of the following holds goods for any triangle ABC ?
View Solution

