If the points $(0, 4) a n d (0, 2)$ are respectively the vertex and focus of a parabola, then find the equation of the parabola.

Video Solution

Text Solution

Verified by Experts

Given that the coordinates, vertex of the parabola (0,4) and focus of the parabola (0,2).

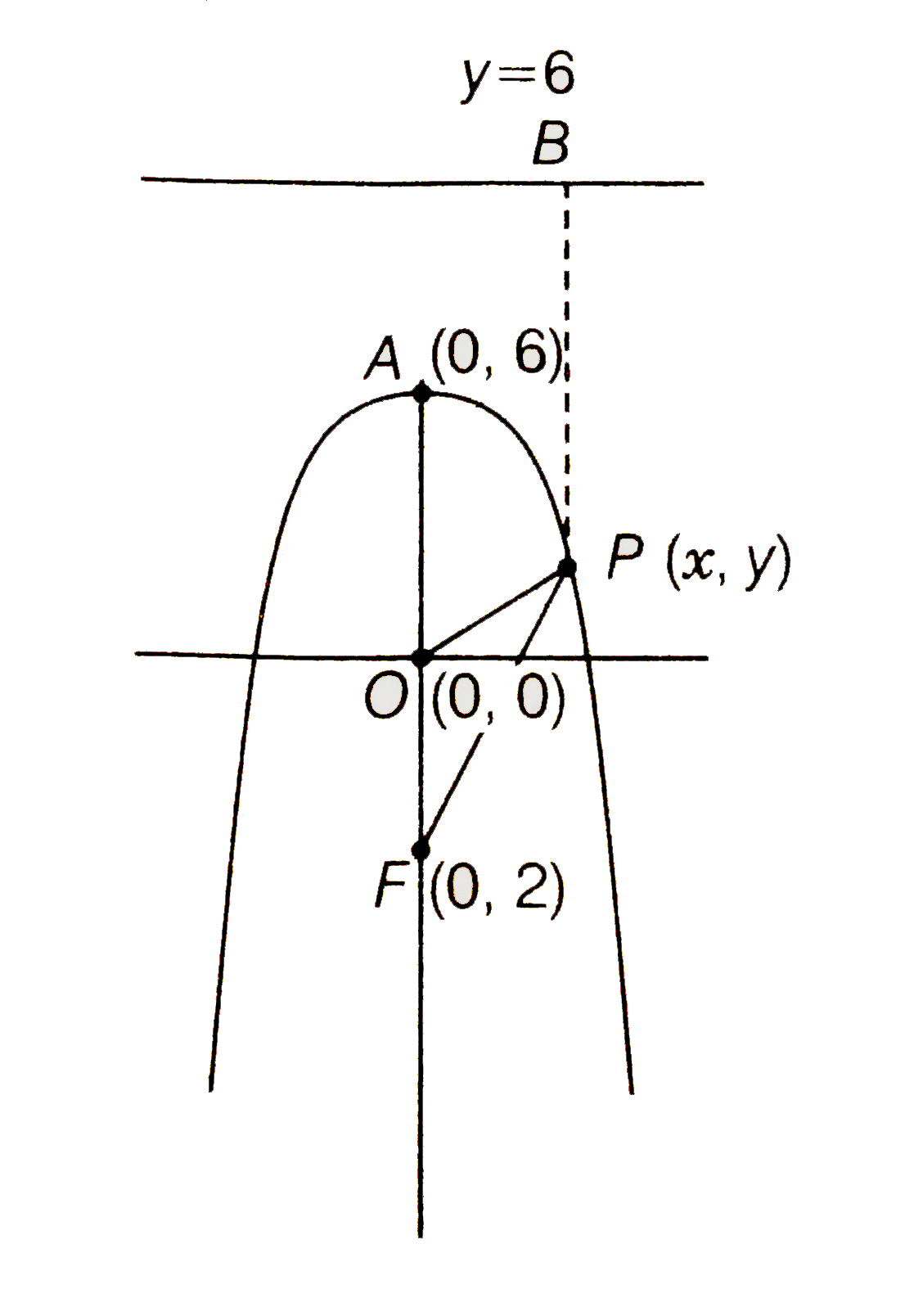
By defination of the parabola, PB=PF
$\Rightarrow ∣ ∣ ∣ \frac{0 + y - 6}{\sqrt{0 + 1}} ∣ ∣ ∣ = \sqrt{{(x - 0)}^{2} + {(y - 2)}^{2}}$ ltbr> $\Rightarrow | y - 6 | = \sqrt{x^{2} + y^{2} - 4 y + 4}$
$\Rightarrow x^{2} + y^{2} - 4 y + 4 = y^{2} + 36 - 12 y$
$\Rightarrow x^{2} + 8 y = 32$

Updated on:21/07/2023

If $(0, 4)$ and $(0, 2)$ are respectively the vertex and focus of a parabola, then its equation is
A $x^{2} + 8 y = 16$
B $x^{2} + 8 y = 32$
C $x^{2} + 16 y = 30$
D $x^{2} - 8 y = 32$
If $(0, 4)$ and $(0, 2)$ are respectively the vertex and focus of a parabola, then its equation is
A $x^{2} + 8 y = 32$
B $y^{2} + 8 x = 32$
C $x^{2} - 8 y = 32$
D $y^{2} - 8 x = 32$
If (0, 3) and (0, 2) are respectively the vertex and focus of a parabola, then its equation, is
A $x^{2} + 8 y = 12$
B $y^{2} + 8 x = 32$
C $x^{2} - 8 y = 32$
D $y^{2} - 8 x = 32$