If the quadratic polynomial is ax2+bx+c , then product of zeroes is ……… .
To find the product of the zeroes of the quadratic polynomial ax2+bx+c, we can follow these steps:
1. Identify the Quadratic Polynomial:
The given polynomial is ax2+bx+c.
2. Understand Zeroes (Roots):
The zeroes (or roots) of the polynomial are the values of x for which the polynomial equals zero. We denote these roots as α and β.
3. Use the Relationship Between Coefficients and Roots:
For any quadratic polynomial of the form ax2+bx+c, the product of the roots α and β can be expressed using Vieta's formulas. According to Vieta's formulas:
α+β=−ba(sum of roots)
α⋅β=ca(product of roots)
4. Conclusion:
Therefore, the product of the zeroes (roots) of the quadratic polynomial ax2+bx+c is given by:
α⋅β=ca
Final Answer:
The product of the zeroes of the quadratic polynomial ax2+bx+c is ca.
---
The given polynomial is ax2+bx+c.
The zeroes (or roots) of the polynomial are the values of x for which the polynomial equals zero. We denote these roots as α and β.
For any quadratic polynomial of the form ax2+bx+c, the product of the roots α and β can be expressed using Vieta's formulas. According to Vieta's formulas:
α+β=−ba(sum of roots)
α⋅β=ca(product of roots)
Therefore, the product of the zeroes (roots) of the quadratic polynomial ax2+bx+c is given by:
α⋅β=ca
The product of the zeroes of the quadratic polynomial ax2+bx+c is ca.
Topper's Solved these Questions
- BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - SELF ASSESSMENT (Objective Type Questions (C) Very Short Answer Type Questions )3videos
POLYNOMIALS
- BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - SELF ASSESSMENT (Objective Type Questions II (Short Answer Type Questions )3videos
POLYNOMIALS
- BOOK - OSWAL PUBLICATIONCHAPTER - POLYNOMIALS EXERCISE - SELF ASSESSMENT (Objective Type Questions (A) Multiple Questions )3videos
POLYNOMIALS
- BOOK - OSWAL PUBLICATIONCHAPTER - PAIR OF LINEAR EQUTIONS IN TWO VARIABLESEXERCISE - Case-Based MCQs15videos
PAIR OF LINEAR EQUTIONS IN TWO VARIABLES
- BOOK - OSWAL PUBLICATIONCHAPTER - PROBABILITYEXERCISE - Self Assessment66videos
PROBABILITY
Similar Questions
Knowledge Check
- Question 1 - Select One or More
If a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
A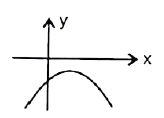 B
B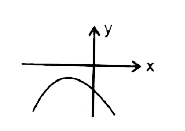 C
C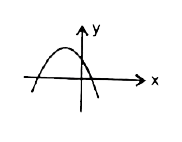 D
D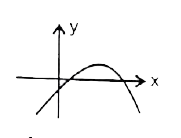
- Question 2 - Select One
If the sum of the zeros of the quadratic polynomial kx2+2x+3k is equal to the product of its zeros then k=?
A13B−13C23D−23 - Question 3 - Select One
A quadratic polynomial whose one zero is −5 and the product of the zeroes is 0 , is .
Ax2+5xBx2−5xCx2+5x+5Dx2−5x+1
Are the following statements 'True' or 'False'? Justify your answer.
(i) If the zeroes of a quadratic polynomial ax2+bx+c are both positive, then a,b and c all have the same sign.
(ii) If the graph of a polynomial intersects the X-axis at only one point, it cannot be a quadratic polynomial.
(iii) If the graph of a polynomial intersects the X-axis at exactly two points, it need not ve a quadratic polynomial.
(iv) If two of the zeroes of a cubic polynomial are zero, then it does not have linear and constant terms.
(v) If all the zeroes of a cubic polynomial are negative, then all the coefficients and the constant term of the polynomial have the same sign.
(vi) If all three zeroes of a cubic polynomial x3+ax2−bx+c are positive, then atleast one of a,b and c is non-negative.
(vii) The only value of k for which the quadratic polynomial kx2+x+k has equal zeroes is 12.View SolutionFind the quadratic polynomial sum and product of whose zeroes are -1 and -20 respectively. Also, find the zeroes of the polynomial so obtained
View SolutionIf one of the zeroes of the cubic polynomial ax3+bx2+cx+d is zero, the product of the other two zeroes is
View SolutionIf one of the zereos of the cubic polynomial x3+ax2+bx+c is -1, then the product of the other two zeroes is
View SolutionFor which of the following graphs of the quadratic expression f(x)=ax2+bx+c, the product of abc is negative
View Solution

