If the sides of a triangle are in A.P., and its greatest angle exceeds the least angle by $α$ , show that the sides are in the ratio $1 + x : 1 : 1 - x$ , , where $x = \sqrt{\frac{1 - cos α}{7 - cos α}}$ Solution in Punjabi

Video Solution

Text Solution

Verified by Experts

The correct Answer is:Thus, the sides are in the ratio $1 + x : 1 : 1 : 1 - x .$

Updated on:21/07/2023

Answer

Step by step video & image solution for If the sides of a triangle are in A.P., and its greatest angle exceeds the least angle by alpha, show that the sides are in the ratio 1+x :1:1-x, , where x = sqrt((1- cos alpha)/(7 - cos alpha)) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 MATHS PROPERTIES AND SOLUTION OF TRIANGLES

Topper's Solved these Questions

PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - SOLVED EXAMPLES
1 Videos
PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHSCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise For Sesssion 1
20 Videos
PRODUCT OF VECTORSBOOK - ARIHANT MATHSCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
52 Videos
SEQUENCES AND SERIESBOOK - ARIHANT MATHSCHAPTER - SEQUENCES AND SERIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
38 Videos

Similar Questions

Match the statements of Column I with values of Column II.

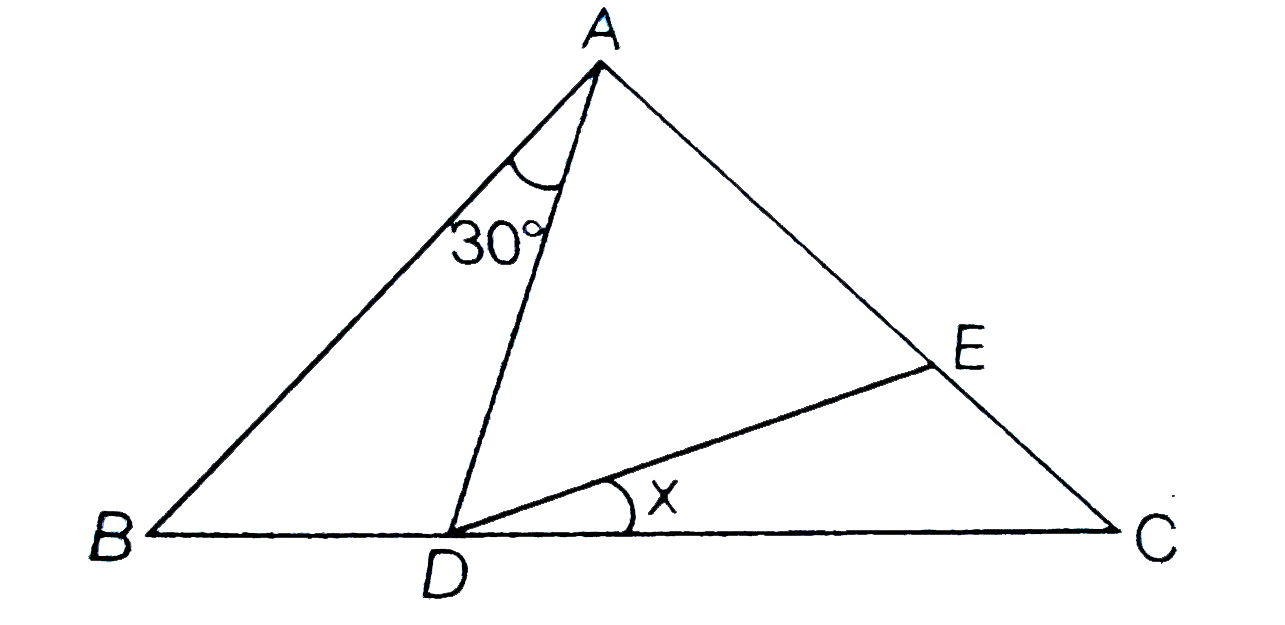
View Solution
In the given figure,if $A B = A C, ∠ B A D = 30^{\circ} and A E = A D,$ then x is equal to

View Solution
Let O be the origin and let PQR be an arbitrary triangle. The point S is such that $¯ ¯¯¯¯ ¯ O P \cdot ¯ ¯¯¯¯ ¯ O Q + ¯ ¯¯¯¯ ¯ O R \cdot ¯ ¯¯¯¯ ¯ O S = ¯ ¯¯¯¯ ¯ O R \cdot ¯ ¯¯¯¯ ¯ O P + ¯ ¯¯¯¯ ¯ O Q \cdot ¯ ¯¯¯¯ ¯ O S = ¯ ¯¯¯¯ ¯ O Q \cdot ¯ ¯¯¯¯ ¯ O R + ¯ ¯¯¯¯ ¯ O P \cdot ¯ ¯¯¯¯ ¯ O S$ Then the triangle PQR has S as its
View Solution
Let a,b,c be in A.P. and $| a | < 1, | b | < 1 | c | < 1 . if x = 1 + a + a^{2} + . . . . to \infty, y = 1 + b + b^{2} + . . . . to \infty and, z = 1 + c + c^{2} + . . . to \infty$ , then x,y,z are in
View Solution
If alpha is the angle which each side of a regular polygon of n sides subtends at its cente,then 1+cos alpha+cos2 alpha+cos3 alpha+......+cos(n-1)a is equal to
View Solution
The sides of a triangle are sin alpha,cos alpha and sqrt(1+sin alpha cos alpha) for some alpha,0
View Solution
If cos^(-1)sqrt(cos alpha)-sin^(-1)sqrt(cos alpha)=x, then the value of sin x is
View Solution
The sides of a triangle are $sin α, cos α and \sqrt{1 + sin α cos α}$ where $0 < α < \frac{π}{2} .$ Then the greatest angle of the triangle is-
View Solution
The sides of the triangle are sin $α$ , cos $α$ and $\sqrt{1 + sin α cos α}$ for some $0 < α < \frac{π}{2}$ . Then the greatest angle of the triangle is
View Solution
In a triangle ABC, if $A = 2 B$ and the side opposite to the angles A, B, C are $α + 1, α - 1$ , and $α$ respectively then $α =$
View Solution
The sides of a triangles are in A.P.and the greatest angle exceeds the least by $90^{\circ}$ , prove that the side are proportional to $(\sqrt{7} + 1), \sqrt{7} and (\sqrt{7} - 1)$
View Solution
The sides of a triangle are $sin α, cos α$ and $\sqrt{1 + sin α cos α}$ for some $0 < α < \frac{π}{2}$ . Then the greatest angle of the triangle is
View Solution
The sides of a triangle are $sin α, cos α and \sqrt{1 + sin α cos α}$ for some $0 < α < \frac{π}{2}$ then the greater angle of the triangle is
View Solution
One side of a square makes an angle $α$ with x axis and one vertex of the square is at origin. Prove that the equations of its diagonals are $x (sin α + cos α) = y (cos α - sin α)$ or $x (cos α - sin α) + y (sin α + cos α) = a$ , where a is the length of the side of the square.
View Solution
If the sides of the triangle sin alpha cos alpha And sqrt(1+ sin alpha cos alpha (while 0 lt alpha lt (pi)/(2) ) Is the greatest angle of the triangle.
View Solution
The sides of a triangle are $sin α, cos α and \sqrt{1 + sin α cos α}$ where $0 < α < \frac{π}{2} .$
Then the greatest angle of the triangle is-
View Solution

ARIHANT MATHS-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

If the sides of a triangle are in A.P., and its greatest angle exceeds...
11:32
Prove that 2sin^2(pi/6) - sec^2(pi/3)= -7/2
02:03
In a triangle the sum of two sides is x and the product of the same is...
05:17
Consider a triangle A B C and let a , b and c denote the lengths of th...
03:54
Solution of differential equation 2xy dy / dx = x^2 + 3y^2 is .
02:52
Let PQR be a triangle of area Delta with a = 2, b = 7//2, and c = 5//2...
04:13
If the angle A ,Ba n dC of a triangle are in an arithmetic propression...
03:49
Let A B C be a triangle such that /A C B=pi/6 and let a , b and c deno...
05:06
A triangle A B C with fixed base B C , the vertex A moves such that co...
04:32
Let A B Ca n dA B C ' be two non-congruent triangles with sides A B=4,...
04:26
A straight line through the vertex P of a triangle P Q R intersects th...
06:17
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Consider the circle x^2 + y^2 = 9 and the parabola y^2 = 8x. They inte...
08:21
Internal bisector of /A of triangle ABC meets side BC at D. A line dra...
04:41
One angle of an isosceles triangle is 120^0 and the radius of its incr...
05:49
In Delta ABC, which one is true among the following ?
01:40
Let a vertical tower A B have its end A on the level ground. Let C be ...
02:45
ABCD is a trapezium such that AB and CD are parallel and BC bot CD. If...
04:13
For a regular polygon, let r and R be the radii of the inscribed and t...
03:37
In triangle A B C , let /c=pi/2dot If r is the inradius and R is circu...
02:21

Home
Ask Doubt
Profile

If the sides of a triangle are in A.P., and its greatest angle exceeds the least angle by α, show that the sides are in the ratio 1+x:1:1−x, , where x=√1−cosα7−cosαSolution in Punjabi

The correct Answer is:Thus, the sides are in the ratio 1+x:1:1:1−x.

Topper's Solved these Questions

Similar Questions

ARIHANT MATHS-PROPERTIES AND SOLUTION OF TRIANGLES -Exercise (Questions Asked In Previous 13 Years Exam)

If the sides of a triangle are in A.P., and its greatest angle exceeds the least angle by $α$ , show that the sides are in the ratio $1 + x : 1 : 1 - x$ , , where $x = \sqrt{\frac{1 - cos α}{7 - cos α}}$ Solution in Punjabi

The correct Answer is:Thus, the sides are in the ratio $1 + x : 1 : 1 : 1 - x .$