If the sum of the distances of a point from two perpendicular lines in a plane is 1, then its locus is a square (b) a circle a straight line (d) two intersecting lines
a square
a circle
a straight line
two intersecting lines
The correct Answer is:A
Let the two perpendicular lines be taken as the coordinates axes. If (h,k) is any point on the locus, then according to the given condition, |h|+|k|=1. Hence, the locus of (h,k) is |x|+|y|=1. This consists of four line segments enclosing a square as shown in the figure.
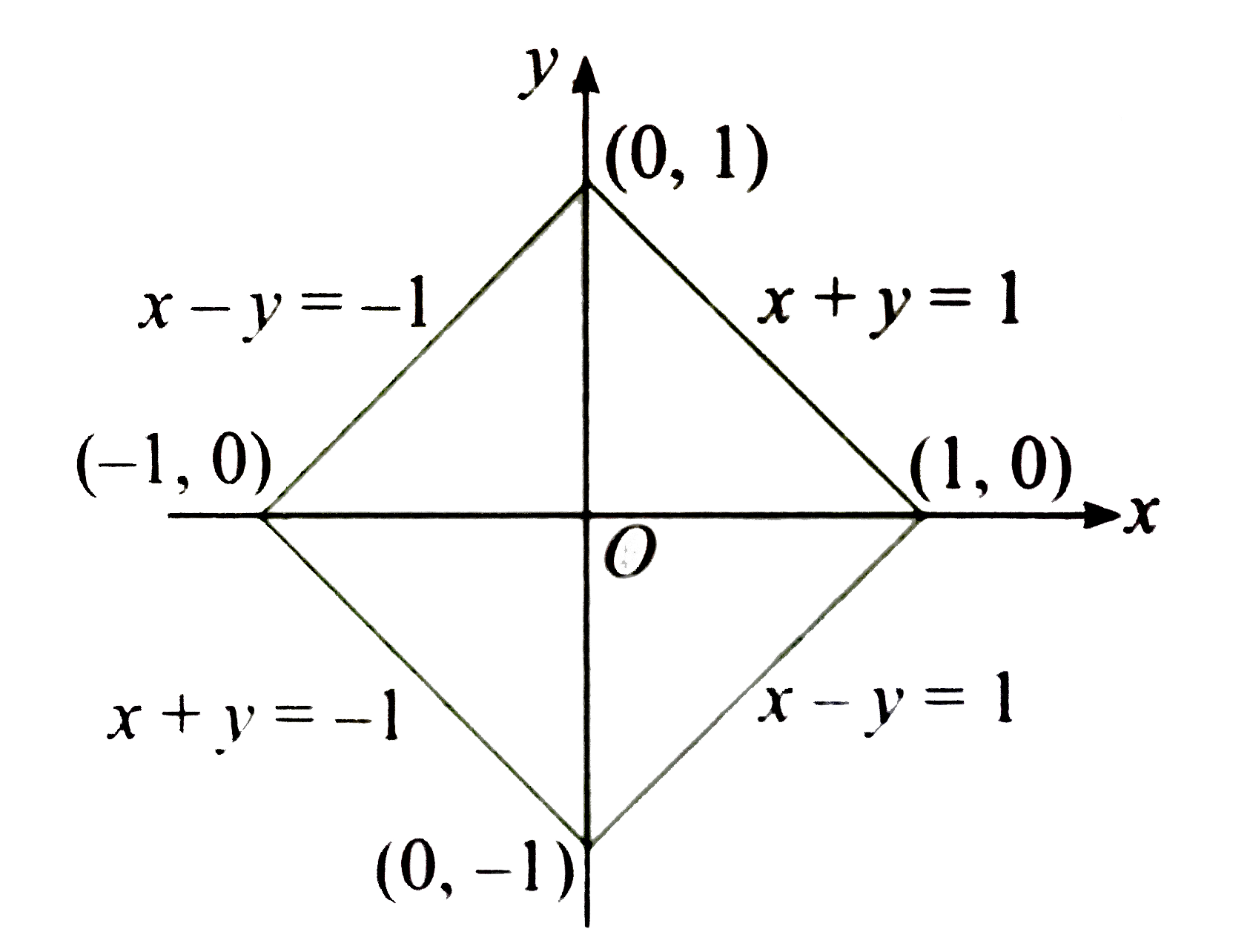
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Comprehension)
Explore 27 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise 2.6
Explore 5 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
Sum of the distances of a point from two perpendicular lines is 3. The area enclosed by the locus of the point is:
View SolutionIn a plane sum of distances of a point with two mutually perpendicular fixed line is one then locus of the point is - 1. square 2. cirlce 3. two intersecting lines 4. straight line
View Solution
Knowledge Check
If the sum of the distances of a point from two perpendicular lines in a planes is 1, then its locus is
Aa squareBa circleCa straight lineDtwo intersecting linesIf the sum of the distances of a point from two perpendicular lines in a planes is 1, then its locus is
Aa squareBa circleCa straight lineDtwo intersecting linesIf the sum of the distance of a point P from two perpendicular lines in a plane, is 1, then the locus of P is a
Aa squareBa circleCa straight lineDtwo intersecting lines
The locus of a point equidistant from two intersecting lines is
View SolutionA point moves in the xy-plane such that the sum of its distances from the two mutually perpendicular lines is always equal to 5 units. The area (in square units) enclosed by the locus of the point is
View SolutionA point moves in the X-Y plne such that the sum of its distance form two mutally perpendicular lines is always equal to 3. The area (in square unit) enclosed by the locus of the point is
View SolutionA point moves in the x-y plane such that the sum of its distances from two mutually perpendicular lines is always equal to √2 units. The area enclosed by the locus of the point is (in sq. units)
View SolutionFind the locus of centres of circles which touch two intersecting lines.
View Solution