If the tangent at (3,−4) to the circle x2+y2−4x+2y−5=0 cuts the circle x2+y2+16x+2y+10=0 in A and B then the midpoint of AB is
Video Solution
Text Solution
The correct Answer is:(−6,−7)
Equation of tangent to circle x2+y2−4x+2y−5=0 at point (3,-4) is
3x−4y−2(x+3)=(y−4)−5=0
or x−3y−15=0 (1)
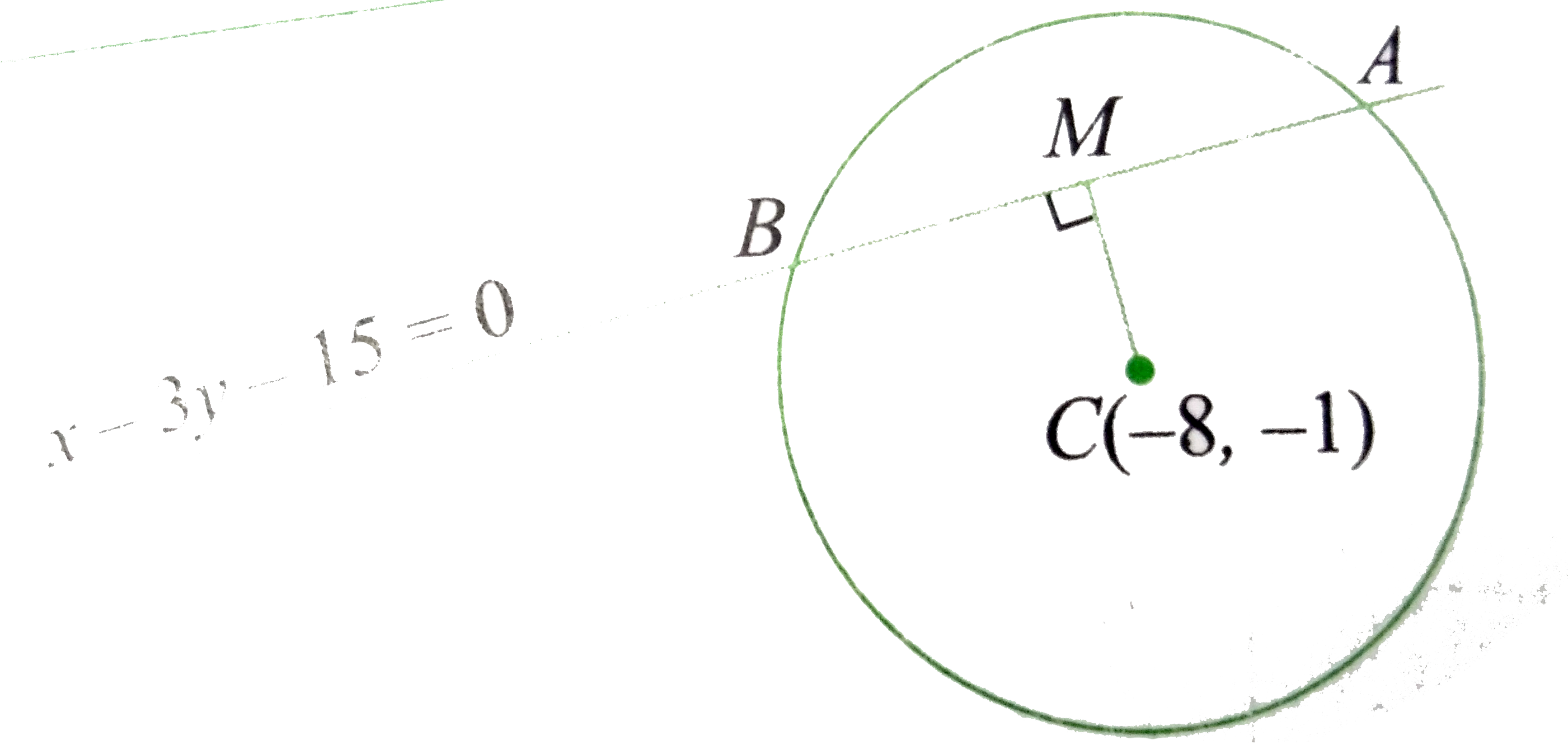
Center of the second circle is C(−8,−1).
Slope of CM is '−3'
Equation of CM is y+1=−3(x+8)
or 3x+y+25=0 (2)
Solving (1) and (2), we get M≡(−6,−7)
|
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.5
Explore 12 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.6
Explore 5 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.3
Explore 18 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Knowledge Check
The length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
A81B29C7D21The length of tangent from (5,1) to the circle x2+y2+6x−4y−3=0 is
A81B29C7D21The tangent at (1,7) to the curve x2=y−6 touches the circle x2+y2+16x+12y+c=0 at
A(6,7)B(-6,7)C(6,-7)D(-6,-7)
Length of tangent from (8,6) to the circle x2+y2−3x−4y+2=0
View SolutionThe length of the tangent from a point on the circle x2+y2+4x–6y−12=0 to the circle x2+y2+4x–6y+4=0 is
View SolutionThe tangents to the circle x2+y2−4x+2y+k=0 at (1,1) is x−2y+1=0 then k=
View SolutionThe tangent at (1,7) to the curve x2=y−6 touches the circle x2+y2+16x+12y+c=0 at
View SolutionThe tangent at (1,7) to the curve x2=y−6 touches the circle x2+y2+16x+12y+c=0 at
View Solution