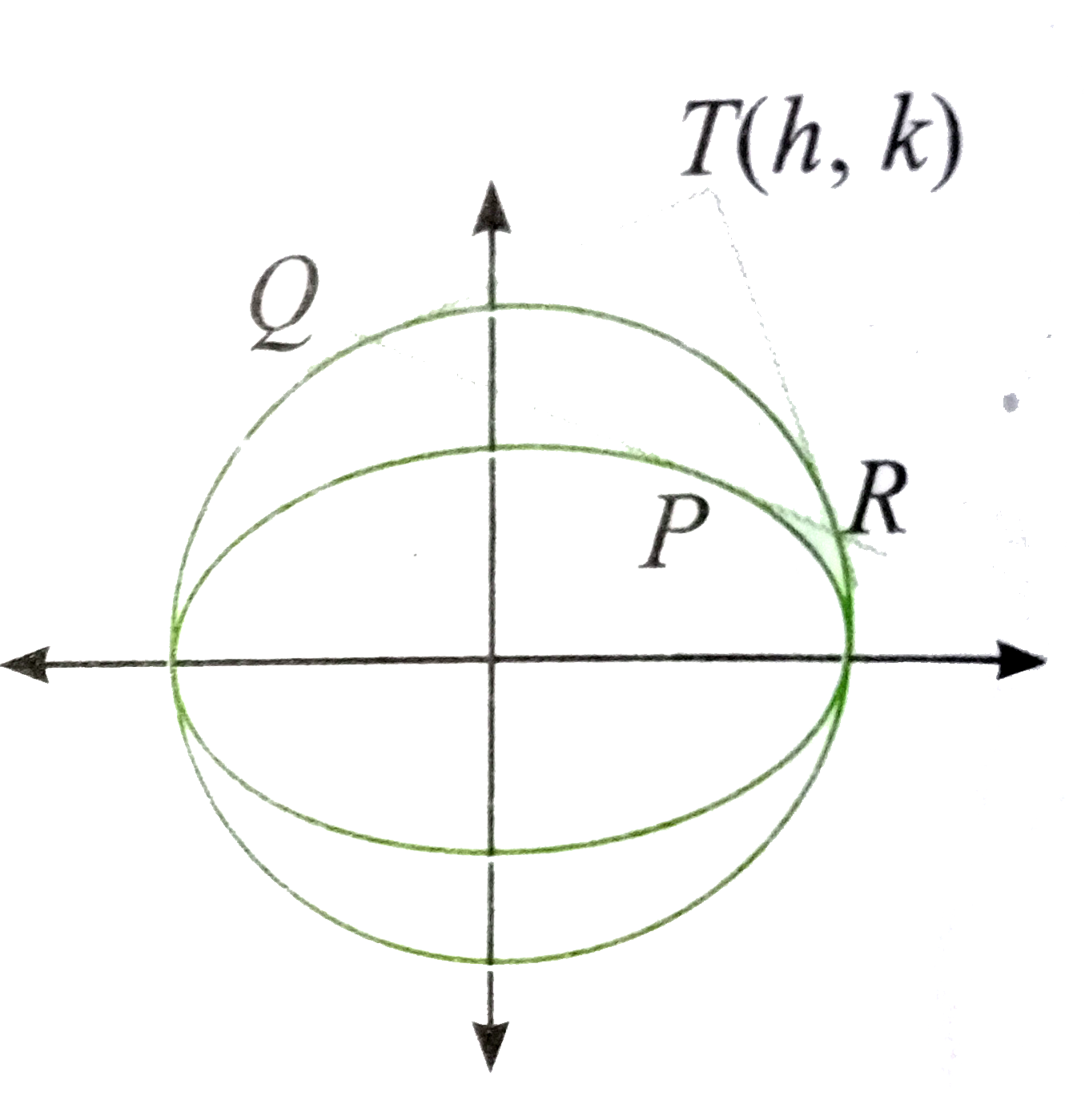
If the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.Solution in Tamil
The correct Answer is:(1,√2,1)
The equation of tangent to the ellipse at a given points is x(1√2)+2y(12)=1
or x+√y=√2 (1)
Now, QR is the chord of contact of the circle x2_y2=1 with respect to the point T(h,k). Then,
QR≡hx+ky+ky=1 (2)
Equations (1) and (2) represent the same straight line. Then comapring the ratio of coefficients, we have, h/1=k/√2=1√2.
Hence (h,k)≡(1/√2)
Similar Questions
Tangents PQandPR are drawn at the extremities of the chord of the ellipse x216+y29=1 , which get bisected at point P(1,1). Then find the point of intersection of the tangents.
View SolutionA variable tangent to the circle x2+y2=1 intersects the ellipse x24+y22=1 at point P and Q. The lous of the point of the intersection of tangents to the ellipse at P and Q is another ellipse. Then find its eccentricity.
View Solutionवृत x2+y2=a2 के किसी बिन्दु P पर स्पर्श रेखा, स्थिर बिन्दु A (a. 0) पर बनी स्पर्श रेखा, T पर मिलती है तथा T को B से मिलाते है, जो A से गुजरने वाले व्यास का दूसरा सिरा है। सिद्ध कीजिए कि AP और BT के प्रतिच्छेद बिन्दुका बिन्दुपथ एक दीर्घवृत्त होगा, जिसकी उत्केन्द्रता 1√2 है।
View SolutionA tangent at a point on the circle x^2+y^2=a^2 intersects a concentric circle C at two points Pa n dQ . The tangents to the circle X at Pa n dQ meet at a point on the circle x^2+y^2=b^2dot Then the equation of the circle is
View SolutionIf the tangent to the ellipse x2+2y2=1 at point P(1√2,12) meets the auxiliary circle at point RandQ , then find the points of intersection of tangents to the circle at QandR.
View SolutionTangents P Qa n dP R are drawn at the extremities of the chord of the ellipse (x^2)/(16)+(y^2)/9=1 , which get bisected at point T(1,1)dot Then find the point of intersection of the tangents.
View SolutionFrom any point on the line y=x+4, tangents are drawn to the auxiliary circle of the ellipse x^2+4y^2=4 . If P and Q are the points of contact and Aa n dB are the corresponding points of Pa n dQ on he ellipse, respectively, then find the locus of the midpoint of A Bdot
View SolutionTangents P Qa n dP R are drawn at the extremities of the chord of the ellipse (x^2)/(16)+(y^2)/9=1 , which get bisected at point T(1,1)dot Then find the point of intersection of the tangents.
View Solution
