If the transformed equation of a curve is 3X2+XY−Y2−7X+Y+7=0 when the axes are translated to the point (1,2), then the original equation of the curve is 3x2+xy−y2−ax+by+c=0, then the ascending order of a,b,c is Solution in Telugu
a,b,c
b,c,a
a,c,b
c,a,b
The correct Answer is:B
Step by step video, text & image solution for If the transformed equation of a curve is 3X^(2) + XY - Y^(2)- 7X + Y +7=0 when the axes are translated to the point (1,2), then the original equation of the curve is 3x^(2) + xy - y^(2) -ax + by+c=0, then the ascending order of a,b,c is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-3
2 Videos
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-4
3 Videos
- TRANSFORMATION OF AXES BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRANSFORMATION OF AXES EXERCISE - SET-1
3 Videos
- THEORY OF EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - THEORY OF EQUATIONSEXERCISE - SET - 4
4 Videos
- TRIGONOMETRIC EQUATIONS BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - TRIGONOMETRIC EQUATIONS EXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
4 Videos
Similar Questions
To remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
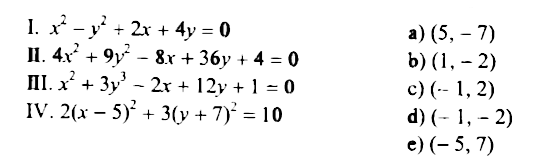
View SolutionA: The transformed equation of x2−y2+2x+4y=0 when the origin is shifted to the point (-1,2) is X2−Y2+3=0.
R: If x,y terms are elimianted form ax2+2hxy+by2+2gx+2fy+c=0 by shifting the origin to (α,β) then the transformed equation is ax2+2hxy+by2+gα+fβ+c=0
View SolutionIf the point (3,-2) is transformed to (-2,1) which the origin is shifted to P, then P=
View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.
View SolutionA : The general solution of sinx=−1 is nπ+(−1)n3π2,n∈Z
R : The principal solution of sin x = 0 lies in [−π/2,π/2]
View SolutionIf origin is shifted to the point (−1,2) then what will be the transformed equation of the curve 2x2+y2−3x+4y−1=0 in the new axes ?
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation of 2x2+y2−4x+4y=0
View SolutionIf the transformed equation of a curve is x2+y2+4x+6y+12=0 when the axes are translated to the point (2,3), then the original equaiton of the curve is
View SolutionLet the equation of the curve x2−xy−y2=11 be transformed to ax2−by2+3x+cy+dxy=e upon shifting the origin to (1,−1) then a2+b2+c2=
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation of 2x2+y2−4x+4y=0
View SolutionIf the transformed equation of a curve is X2+2√3XY−Y2=2a2 ,when the axes are rotated through an angle of 60∘ ,then the original equation
View SolutionIf the transformed equation of a curve is x2+y2=16 when the axes are translated to the point (- 1, 2 ) then find the original equation of the curve.
View SolutionIf 3X2+XY−Y2−7X+Y+7=0 is the transformed equation of a curve, when the axes are translated to the point (1,2), then find the original equation of the curve.
View SolutionIf the transformed equation of curve is
X2+2Y2+16=0 when the axes are translated to the point (-1,2) then find the original equation of the curve.
View SolutionIf the transformed equation of curve is
X2+Y2=4 when the axes are translated to the point (-1,2) then find the original equation of the curve.
View Solution
