A: The transformed equation of x2−y2+2x+4y=0 when the origin is shifted to the point (-1,2) is X2−Y2+3=0.
R: If x,y terms are elimianted form ax2+2hxy+by2+2gx+2fy+c=0 by shifting the origin to (α,β) then the transformed equation is ax2+2hxy+by2+gα+fβ+c=0 Solution in Telugu
Both A and R are true and R is the correct explanation of A.
Both A and R are true but R is not the correct explanation of A.
A is true but R is false
A is false but R is false
The correct Answer is:A
Step by step video, text & image solution for A: The transformed equation of x^(2) - y^(2) + 2x + 4y=0 when the origin is shifted to the point (-1,2) is X^(2) - Y^(2) +3=0. R: If x,y terms are elimianted form ax^(2) + 2hxy +by^(2) + 2gx + 2fy +c=0 by shifting the origin to (alpha, beta) then the transformed equation is ax^(2)+ 2hxy + by^(2) + galpha + f beta + c=0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRANSFORMATION OF AXES Book:DIPTI PUBLICATION ( AP EAMET)Chapter:TRANSFORMATION OF AXES Exercise:SET-3
Explore 2 Videos
- THEORY OF EQUATIONSBook:DIPTI PUBLICATION ( AP EAMET)Chapter:THEORY OF EQUATIONSExercise:SET - 4
Explore 4 Videos
- TRIGONOMETRIC EQUATIONS Book:DIPTI PUBLICATION ( AP EAMET)Chapter:TRIGONOMETRIC EQUATIONS Exercise:EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET - 4
Explore 4 Videos
Similar Questions
To remove the first degree terms in the following equation origin should be shifted to the another point then calculate the new origins is
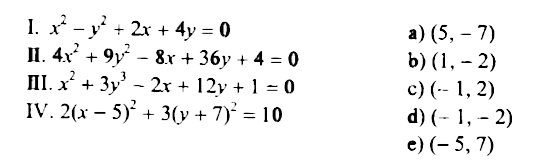
View SolutionA : the equation whose roots are multiplied by 2 of those of x5−2x4+3x3−2x2+4x+3=0 is x5−4x4+12x3−16x2+64x+96=0.
R: the equation whose roots are multiplied by k of those of f(x) = 0 is f(x/k) = 0.
View SolutionA : The general solution of sinx=−1 is nπ+(−1)n3π2,n∈Z
R : The principal solution of sin x = 0 lies in [−π/2,π/2]
View SolutionThe first degree terms of ax^(2)+2hxy+by^(2)+2gx+2fy+c=0 are removed by shifting origin to (alpha,beta) .The new equation as
View SolutionWhen the origin is shifted to a suitable point, the equation 2x^(2)+y^(2)-4x+4y=0 transformed as 2x^(^^)2+y^^2-8x+8y+18=0^(@) The point to which origin was shifted is
View SolutionIf origin is shifted to the point (−1,2) then what will be the transformed equation of the curve 2x2+y2−3x+4y−1=0 in the new axes ?
View SolutionTransform the equation 2x2+y2−4x+4y=0 to parallel axes when the origin is shifted to the point (1,-2)
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation of 2x2+y2−4x+4y=0
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation x2+y2+2x−4y+1=0.
View SolutionThe condition that the equation ax2+2hxy+by2+2gx+2fy+c=0 can take the form ax2−2hxy+by2=0, when shifting the origi is
View SolutionThe transformed equation of ax2+2hxy+by2+2gx+2fy+c=0 when the axes are rotated through an angle 90∘ is
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation x2+y2+2x−4y+1=0.
View SolutionWhen the origin is shifted to (-1,2) by the translation of axes, find the transformed equation of 2x2+y2−4x+4y=0
View SolutionFind the transformed equation of
2x2+y2−4x+4y=0 when the origin is shifted to the point (-1,2).
View SolutionThe transformed equation of x2−y2+2x+4y=0 when the origin is shifted to the point (-1, 2) is
View Solution