If the velocity of a body moving in a straight line is proportional to the square root of the distance traversed, then it moves with
variable force
constant force
zero force
zero acceleration
The correct Answer is:B
To solve the problem, we need to analyze the relationship between velocity, distance, and acceleration based on the information given. Let's break it down step by step.
1. Understanding the Relationship:
We are given that the velocity v of a body is proportional to the square root of the distance s traversed. This can be mathematically expressed as:
v∝√s
Therefore, we can write:
v=k√s
where k is a constant of proportionality.
Hint: Remember that proportionality means we can express one quantity as a constant multiplied by another.
2. Finding Acceleration:
Acceleration a is defined as the rate of change of velocity with respect to time:
a=dvdt
To find a, we need to differentiate v with respect to t.
3. Using the Chain Rule:
We can apply the chain rule for differentiation. Since v=k√s, we differentiate it with respect to t:
dvdt=ddt(ks1/2)=k⋅12s−1/2⋅dsdt
Here, dsdt is the velocity v.
Hint: The chain rule allows us to differentiate composite functions. Remember to express dsdt in terms of v.
4. Substituting for Velocity:
Substituting v=k√s into the equation:
a=12ks−1/2⋅v
Replacing v with k√s:
a=12ks−1/2⋅(k√s)=12k2
Notice that s−1/2 and √s cancel out.
Hint: When substituting, ensure that you keep track of the variables and their relationships.
5. Conclusion:
The expression for acceleration a simplifies to a constant value 12k2. Since a is constant, this implies that the force acting on the body, given by F=m⋅a, is also constant (assuming mass m is constant).
Therefore, the body moves with constant force.
Hint: Remember that constant acceleration implies constant force when mass is constant.
Final Answer:
The body moves with constant force.
We are given that the velocity v of a body is proportional to the square root of the distance s traversed. This can be mathematically expressed as:
v∝√s
Therefore, we can write:
v=k√s
where k is a constant of proportionality.
Acceleration a is defined as the rate of change of velocity with respect to time:
a=dvdt
To find a, we need to differentiate v with respect to t.
We can apply the chain rule for differentiation. Since v=k√s, we differentiate it with respect to t:
dvdt=ddt(ks1/2)=k⋅12s−1/2⋅dsdt
Here, dsdt is the velocity v.
Substituting v=k√s into the equation:
a=12ks−1/2⋅v
Replacing v with k√s:
a=12ks−1/2⋅(k√s)=12k2
Notice that s−1/2 and √s cancel out.
The expression for acceleration a simplifies to a constant value 12k2. Since a is constant, this implies that the force acting on the body, given by F=m⋅a, is also constant (assuming mass m is constant).
The body moves with constant force.
Topper's Solved these Questions
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DERIVATIVE AS A RATE MEASURER BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DERIVATIVE AS A RATE MEASURER EXERCISE - Exercise
26 Videos
- DEFINITE INTEGRALSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DEFINITE INTEGRALSEXERCISE - Chapter Test 2
56 Videos
- DIFFERENTIAL EQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Chapter Test
30 Videos
Similar Questions
If a point is moving in a line so that its velocity at time t is proportional to the square of the distance covered, then its acceleration at time t varies as
View SolutionIf a particle is moving such that the velocity acquired is proportional to the square root of the distance covered, then its acceleration is
View Solution
Knowledge Check
The variataion of velocity of a particle moving along a straight line is illustrated in the following Fig. 3.1. The distance traversed by the particle in 4 seconds is
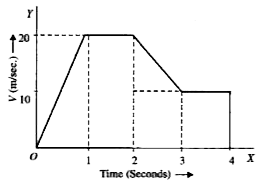 A60 mB25 mC55 mD30 m
A60 mB25 mC55 mD30 m
If average velocity of particle moving on a straight line is zero in a time interval, then
View SolutionThe velocity of a particle moving in a straight line is directly proportional to 3/4th power of time elapsed. How does its displacement and acceleration depend on time?
View SolutionThe position of a particle moving on a straight line is proportional to the cube of the time elapsed. How does the acceleration of the particle depend on time elapsed?
View SolutionThe velocity-time graph of a body moving in a straight line is shown in Fig. Find the displacement and distance travelled by the body in 10 sec.
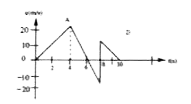
View SolutionThe velocity time graph of a body moving in a straight line is shown in the figure. The displacement and distance travelled by the body in 6 sec are respectively.

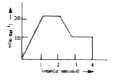
View SolutionThe variation of velocity of a particle moving along a straight line is shown in the figure. The distance travelled by the particle in 4s is
View SolutionThe velocity of a body moving in a straight line is increased by applying a constant force F, for some distance in the direction of the motion. Prove that the increase in the kinetic energy of the body is equal to the work done by the force on the body.
View Solution
