If two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3. Solution in Bengali
The correct Answer is:49198
2m+2n+1=(3−1)m+(3−1)n+1
=3k+(−1)m+(−1)n+1
This is divisible by 3 if both m and n are even.
∴ Required probabaility = .50C2.100C2=50×49100×99=49198
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.3
7 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - MCQ
54 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
AandB are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is p= a.√11−3 b. √10−3 c. 14<p<12 d.none
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
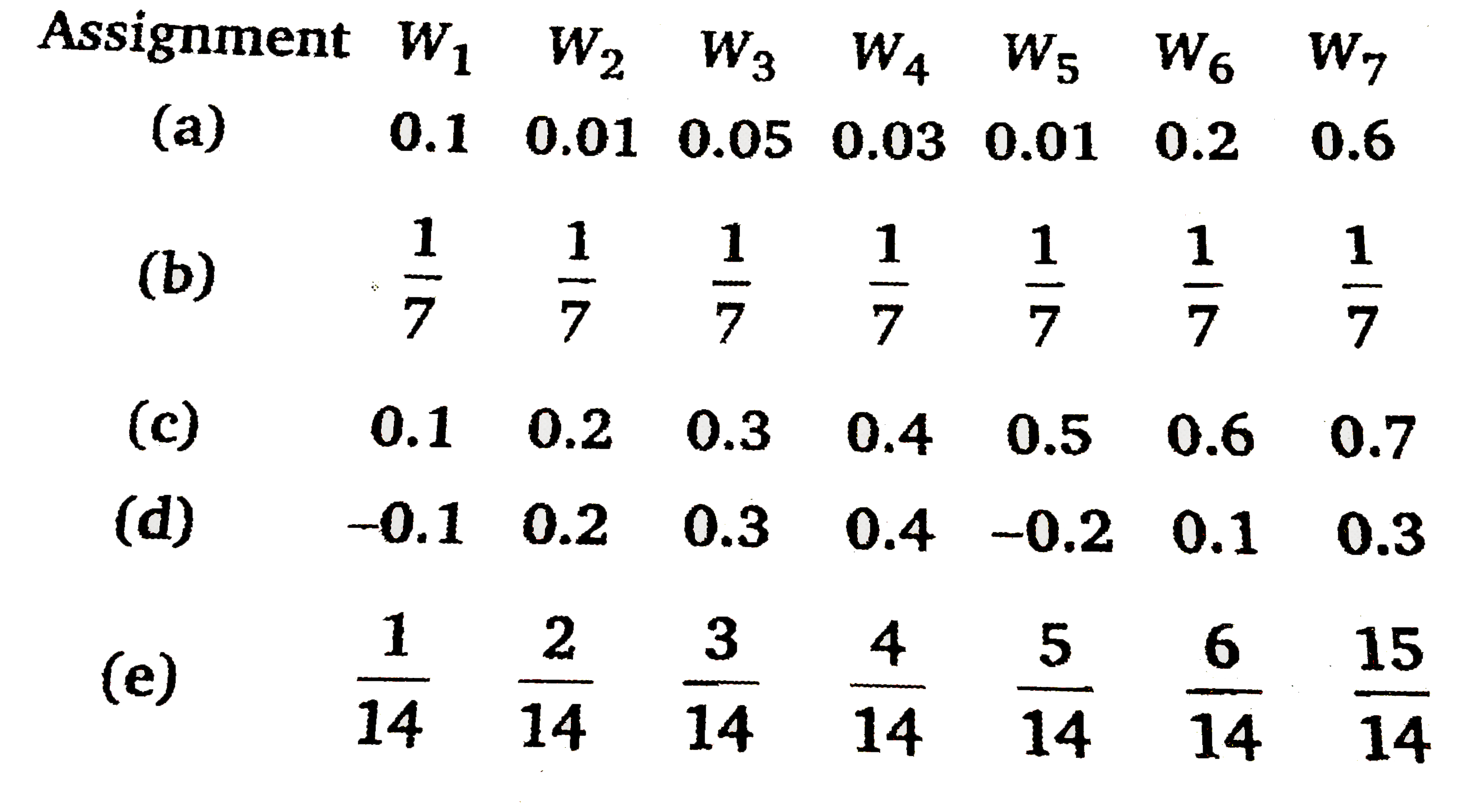
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
View SolutionLet n=10λ+r,whereλ,r∈N,0≤r≤9. A number a is chosen at random from the set {1, 2, 3,…, n} and let pn denote the probability that (a2−1) is divisible by 10.
If 1≤r≤8, then np_n equals
View SolutionIf the integers m and n are chosen at random between 1 and 100, then the probability that a number of the form 7m+7n is divisible by 5, equals :
View SolutionIf the integers m and n are chosen at random between 1 and 100, then atmost distinct numbers of the form 7m+7n is divisible by 5 equals to :
View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
View SolutionIf the integers m and n are chosen at random between 1 and 100, then atmost distinct numbers of the form 7m+7n is divisible by 5 equals to :
View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
View SolutionIf two distinct numbers m and n are chosen at random form the set {1, 2, 3, …, 100}, then find the probability that 2m+2n+1 is divisible by 3.
View Solution3 distinct integers are selected at random form 1, 2, 3, …, 20. find out the probability that the sum is divisible by 5
View Solution
