If two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity). Solution in Bengali
The correct Answer is:59
Total number of cases n(S) = 36
Since ωab = 1, ab must be multiple of 3.
So, at least one of a and b must be multiple of 3.
If none of the dices shows 3 or 6, number of cases is 4×4=16.
So, number of cases in which at least one of the dices shows 3 or 6 is 36 - 16 = 20.
∴ Required probability = 2036=59
Topper's Solved these Questions
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.3
7 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - MCQ
54 Videos
- PROBABILITY I BOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY I EXERCISE - Exercise 9.1
6 Videos
- PROBABILITYBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITYEXERCISE - All Questions
470 Videos
- PROBABILITY IIBOOK - CENGAGE PUBLICATIONCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
Similar Questions
AandB are two candidates seeking admission in IIT. The probability that A is selected is 0.5 and the probability that AandB are selected is at most 0.3. Is it possible that the probability of B getting selected is 0.9?
View SolutionA sample space consists of 3 sample points with associated probabilities given as 2p,p2,4p−1. Then the value of p is p= a.√11−3 b. √10−3 c. 14<p<12 d.none
View SolutionWhich of the following cannot be valid assignment of probabilities for outcomes of sample space S={W1,W2,W3,W4,W5,W6,W7}
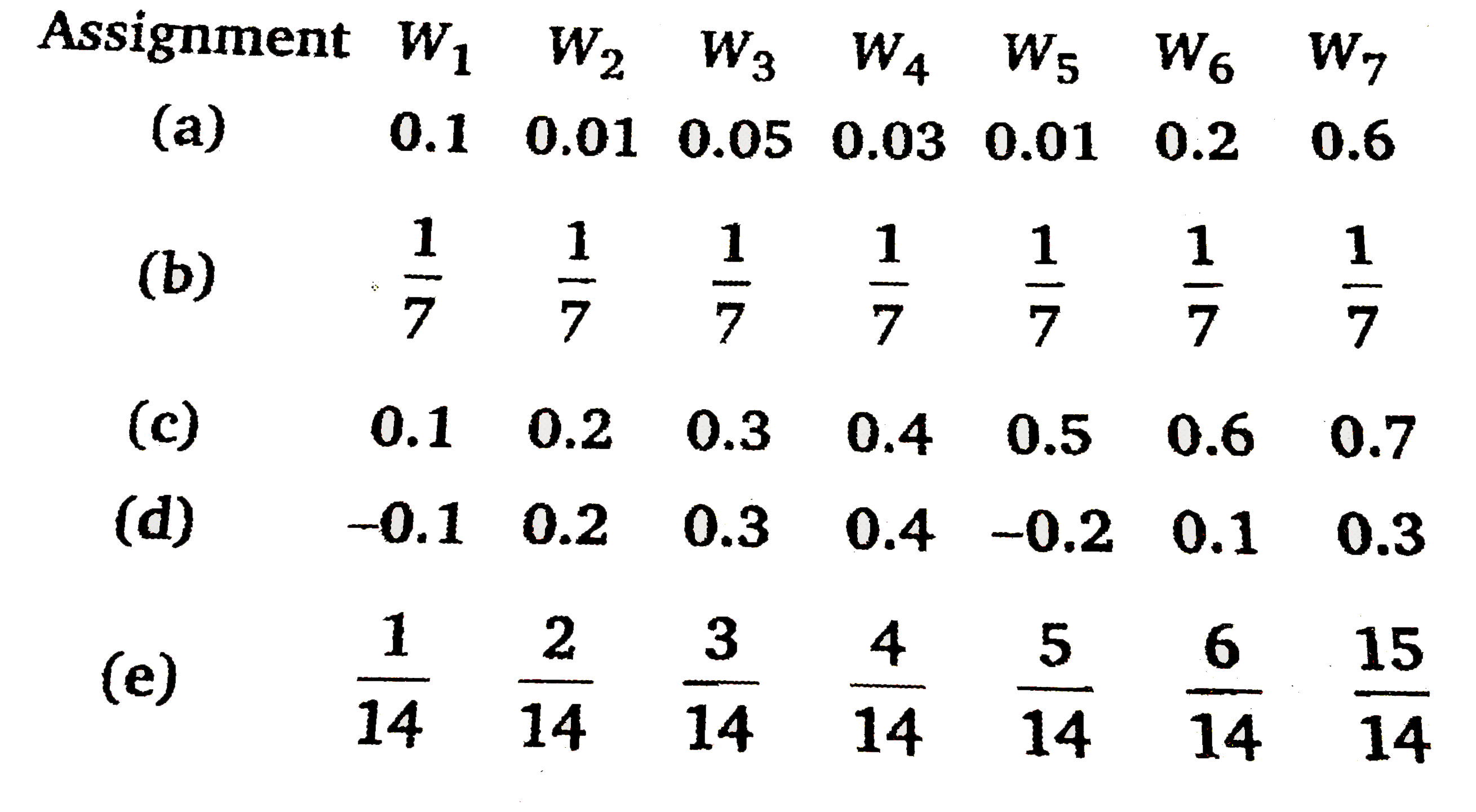
View SolutionA coin is tossed three times, consider the following events. A : ‘No head appears’, B: ‘Exactly one head appears’ and C: ‘Atleast two appear’. Do they form a set of mutually exclusive and exhaustive events?
View SolutionLet EandF be two independent events. The probability that exactly one of them occurs is 1125 and the probability if none of them occurring is 225. If P(T) denotes the probability of occurrence of the event T, then (a) P(E)=45,P(F)=35 (b) P(E)=15,P(F)=25 (c) P(E)=25,P(F)=15 (d) P(E)=35,P(F)=45
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View Solutionमाना कि ω इकाई का एक सम्मिश्र घनमूल है जहाँ ω≠ है। एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि r1,r2 और r3 पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते है तो ωr1+ωr2+ωr3=0 होने की प्रायिकता है-
View SolutionEvaluate: ∣∣ ∣ ∣∣1111ω2ω1ωω2∣∣ ∣ ∣∣ (where ω is an imaginary cube root of unity ).
View SolutionIf ω is a complex cube -root of unity and A'=[ωω] and B'=[1ω], then: AB=
View Solutionयदि दो निष्पक्ष पासों को फैंका जाता है, तब इस बात कि सप्रतिबंध प्रायिकता क्या है कि पहले पासे पर 6 आए, जबकि यह दिया हुआ है कि पासों पर आए अंकों का योगफल 8 रहे?
View SolutionTwo dices are rolled and numbers r1 and r2 are chosen. Let 1+ωr1+ωr2=λ (where ω is a complex cube root of unity). Then
View Solution(1+w)7=A+Bw where w is the imaginary cube root of of a unity and A,B∈R, find the ordered pair (A, B).
View Solutionमाना कि ω, इकाई का एक सम्मिश्र धनमूल हैं जहां ω≠1 एक निष्पक्ष पांसा तीन बार उछाला जाता है। यदि r1,r2 एवं r2 पांसे के उछाले जाने पर प्राप्त अंक दर्शाते है तो ωr1+ωr2+ωr3=0 होने की प्रायिकता निम्न है
View Solutionमाना ω इकाई का एक सम्मिश्र घनमूल है, जहाँ ω≠1. एक निष्पक्ष पाँसा तीन बार उछाला जाता है। यदि r1,r2 एवं r3 पाँसे के उछाले जाने पर प्राप्त अंक दर्शाते हैं, तो ωr1+ωr2+ωr3=0 की प्रायिकता निम्न है
View SolutionIf two fair dices are thrown and digits on dices are a and b, then find the probability for which ωab=1, (where ω is a cube root of unity).
View Solutionमाना कि ω, इकाई का एक सम्मिश्र धनमूल हैं जहां ω≠1 एक निष्पक्ष पांसा तीन बार उछाला जाता है। यदि r1,r2 एवं r2 पांसे के उछाले जाने पर प्राप्त अंक दर्शाते है तो ωr1+ωr2+ωr3=0 होने की प्रायिकता निम्न है
View Solution
